题目内容
16．关于x的不等式（2a-b）x+a-2b＞0的解为x$＜\frac{10}{7}$，则不等式ax＞b的解为x＜$\frac{9}{8}$．分析 先求出不等式的解集，根据不等式的解集为x$＜\frac{10}{7}$，建立关于a、b的关系式，求出a、b的比，再据此解答不等式ax＞b的解集．
解答 解：由关于x的不等式（2a-b）x+a-2b＞0解得
x＜$\frac{2b-a}{2a-b}$或x＞$\frac{2b-a}{2a-b}$，
因为x$＜\frac{10}{7}$，
所以2a-b＜0，即2a＜b，
所以$\frac{2b-a}{2a-b}$=$\frac{10}{7}$，
20a-10b=14b-7a，
∴27a=24b，即9a=8b，
∵2a＜b，
即2a＜$\frac{9}{8}$a，
∴a＜0，
因为ax＞b，且a＜0，
解得：x＜$\frac{9}{8}$．
故答案是：x＜$\frac{9}{8}$．
点评 本题是一个方程与不等式的综合题目，要充分利用题目中的隐含条件---不等号的方向发生了改变，确定a、b同号，再解关于x的不等式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．为了解我市九年级学生升学考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：40分；B：39-35分；C：34-30分；D：29-20分； E：19-0分） 统计如表．根据上面提供的信息，回答下列问题：
（1）在统计表中，a的值为32，b的值为10；
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数”．请问：甲同学的体育成绩应在B分数段内（填相应分数段的字母）．
（3）若把成绩在35分以上（含35分）定为优秀，则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有6400名．
| 分数段 | 人数（人） | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数”．请问：甲同学的体育成绩应在B分数段内（填相应分数段的字母）．
（3）若把成绩在35分以上（含35分）定为优秀，则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有6400名．
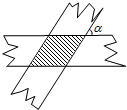如图：两张宽度都为1cm的纸条交叉重叠在一起，两张纸条交叉的夹角为α（见图中的标注），则重叠（阴影）部分的面积表示为$\frac{1}{sinα}$．
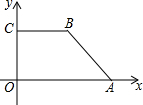如图所示的平面直角坐标系中，在直角梯形OABC中，CB∥OA，CB=8，OC=6，∠OAB=45°．