题目内容
15.已知:直线y=-x+6与双曲线y=$\frac{k}{x}$交于第一象限P,Q两点.(1)若点P的横坐标为2,求k的值,并直接写出不等式-x+6>$\frac{k}{x}$的解集;
(2)若△OPQ(O为坐标原点)为等边三角形,求k的值.
分析 (1)由于直线y=-x+6与双曲线y=$\frac{k}{x}$交于第一象限P,Q两点,点P的横坐标为2,代入y=-2+6=4,求得P(2,4),于是得到k=8,解方程组得到Q(4,2),即可得到结论;
(2)由于直线y=-x+6与双曲线y=$\frac{k}{x}$交于第一象限P,Q两点,解方程组求得P、Q的坐标,根据两点间的距离公式得PQ=$\sqrt{72-8k}$,OQ=OP=$\sqrt{36-2k}$,根据等边三角形的边相等列方程求得结果.
解答 解:(1)∵直线y=-x+6与双曲线y=$\frac{k}{x}$交于第一象限P,Q两点,点P的横坐标为2,
∴y=-2+6=4,
∴P(2,4),
∴4=$\frac{k}{2}$,
∴k=8,
∴反比例函数的解析式为:y=$\frac{8}{x}$,
解$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{8}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,或$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
∴Q(4,2),
∴不等式-x+6>$\frac{k}{x}$的解集:2<x<4;
(2)∵直线y=-x+6与双曲线y=$\frac{k}{x}$交于第一象限P,Q两点,
解$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{k}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=3+\sqrt{9-k}}\\{{y}_{1}=3-\sqrt{9-k}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3-\sqrt{9-k}}\\{{y}_{2}=3+\sqrt{9-k}}\end{array}\right.$,
根据两点间的距离公式得PQ=$\sqrt{72-8k}$,OQ=OP=$\sqrt{36-2k}$,
∵△OPQ为等边三角形,
∴PQ=OQ=OP,
∴$\sqrt{72-8k}$=$\sqrt{36-2k}$,
解得:k=6.
点评 本题考查了反比例函数和一次函数的交点问题,两点间的距离公式,等边三角形的性质,熟练掌握两点间的距离公式是解题的关键.

| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问:甲同学的体育成绩应在B分数段内(填相应分数段的字母).
(3)若把成绩在35分以上(含35分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有6400名.
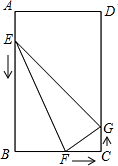 如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).
如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).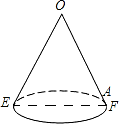 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.
如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.