题目内容
8.计算:(1)18-6÷(-2)×(-$\frac{1}{3}$)
(2)-24-32$÷\frac{9}{4}$×(-$\frac{3}{2}$)2
(3)|-3|+(-1)2015×(π-3)0-(-$\frac{1}{2}$)-3
(4)($\frac{1}{4}$a2b)•(-2ab2)2•(2a3b4)
分析 (1)先算乘除法,再算减法即可解答本题;
(2)根据幂的乘方、有理数的乘除法和减法进行计算即可解答本题;
(3)根据绝对值、幂的乘方、零指数幂、负整数指数幂即可解答本题;
(4)根据积的乘方、同底数幂的乘法即可解答本题.
解答 解:(1)18-6÷(-2)×(-$\frac{1}{3}$)
=18-6×$(-\frac{1}{2})×(-\frac{1}{3})$
=18-1
=17;
(2)-24-32$÷\frac{9}{4}$×(-$\frac{3}{2}$)2
=-16-9×$\frac{4}{9}×\frac{9}{4}$
=-16-9
=-25;
(3)|-3|+(-1)2015×(π-3)0-(-$\frac{1}{2}$)-3
=3-1×1-(-8)
=3-1+8
=10;
(4)($\frac{1}{4}$a2b)•(-2ab2)2•(2a3b4)
=$(\frac{1}{4}{a}^{2}b)•(4{a}^{2}{b}^{4})•(2{a}^{3}{b}^{4})$
=2a7b9.
点评 本题考查整式的混合运算、零指数幂、负整数指数幂、幂的乘方、积的乘方,解题的关键是明确它们各自的计算方法.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.已知2x3yn-1和-x3my2是同类项,则式子m-n的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
20.已知y是x的一次函数,其部分对应值如下表:
(1)求这个一次函数的表达式,并补全表格;
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
| x | -3 | 0 | 3 | 5 |
| y | -4 | 2 | 8 | 12 |
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
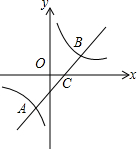 如图,直线y=x-1与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,与x轴交于点C,
如图,直线y=x-1与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,与x轴交于点C,
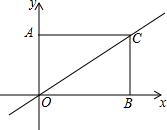 有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.
有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.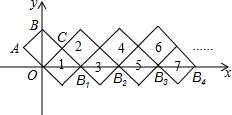 如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.
如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.