题目内容
18.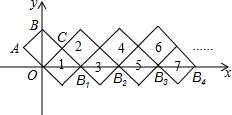 如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.
如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.
分析 分奇数、偶数讨论,即可得出结论.
解答  解:当n是奇数时,第n个正方形右侧顶点的横坐标为$\frac{n+1}{2}$$\sqrt{2}$,
解:当n是奇数时,第n个正方形右侧顶点的横坐标为$\frac{n+1}{2}$$\sqrt{2}$,
当n是偶数时,第n个正方形右侧顶点的横坐标为$\frac{\sqrt{2}}{2}$+$\frac{n\sqrt{2}}{2}$=$\frac{n+1}{2}$$\sqrt{2}$
故答案为$\frac{n+1}{2}$$\sqrt{2}$.
点评 本题考查正方形的性质、坐标与图形的性质等知识,解题的关键是学会分类讨论,掌握从一般到特殊探究规律的方法,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.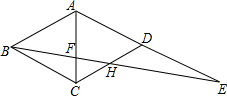 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )| A. | 2 | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{13}{3}$ |
8.在2,$\frac{1}{2}$,0,-2四个数中,最大的数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
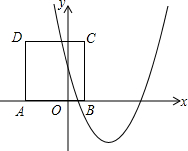 如图,正方形ABCD的边AB在x轴上,点A(-2,0)、点B(1,0),抛物线y=x2-4x+m与正方形有两个交点时,则m的取值范围是-12<m<5.
如图,正方形ABCD的边AB在x轴上,点A(-2,0)、点B(1,0),抛物线y=x2-4x+m与正方形有两个交点时,则m的取值范围是-12<m<5.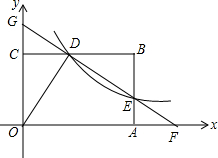 如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.
如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14. 如图,其中邻补角共有3对.
如图,其中邻补角共有3对. 如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.
如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.