题目内容
1.水龙头关闭不严会造成漏水,通过一次调查发现漏水量与漏水时间的关系如表:| 时间 (分钟) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 水量 (毫升) | 0 | 21 | 41 | 59 | 79 | 101 | 121 |
分析 先根据众数的定义求出表中每间隔5分钟漏水量的众数,再利用样本估计总体的思想估算出这种漏水状态下一天该水龙头的漏水量.
解答 解:由表格中数据可知,表中每间隔5分钟的漏水量(毫升)分别为:21,20,18,20,22,20,
20出现了3次,次数最多,所以众数为20,
则这种漏水状态下一天该水龙头的漏水量为:20×(24×60÷5)=5760(毫升).
点评 本题考查了众数的定义以及用样本估计总体的思想,众数是一组数据中出现次数最多的数据.求出表中每间隔5分钟漏水量的众数是解题的关键.

练习册系列答案
相关题目
6.若反比例函数y=$\frac{k}{x}$的图象过点(-3,1),则该图象还经过( )
| A. | (1,3) | B. | (3,-1) | C. | (3,1) | D. | (-1,-3) |
6.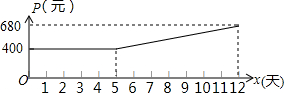 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.| 时间x(天) | 2 | 4 |
| 每天产量y(吨) | 24 | 28 |
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
11.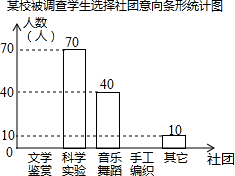 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
根据统计图表中的信息,解答下列问题:
(1)本次调查的学生总人数为200人;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为72°;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为420人.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
(1)本次调查的学生总人数为200人;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为72°;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为420人.
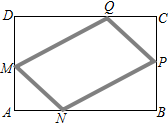 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大.
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大.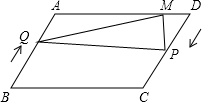 已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).
已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).