题目内容
9.计算(1)(-6)2×($\frac{2}{3}$-$\frac{1}{2}$)-23
(2)2×($\sqrt{5}$+3)+3-2×$\sqrt{5}$.
分析 (1)根据实数的运算顺序,首先计算乘方和小括号里面的算式,然后从左向右依次计算,求出算式(-6)2×($\frac{2}{3}$-$\frac{1}{2}$)-23的值是多少即可.
(2)首先应用乘法分配律,求出2×($\sqrt{5}$+3)的值是多少,然后计算乘法,最后应用加法交换律和加法结合律,求出算式2×($\sqrt{5}$+3)+3-2×$\sqrt{5}$的值是多少即可.
解答 解:(1)(-6)2×($\frac{2}{3}$-$\frac{1}{2}$)-23
=36×$\frac{1}{6}$-8
=6-8
=-2
(2)2×($\sqrt{5}$+3)+3-2×$\sqrt{5}$
=2$\sqrt{5}$+6+3-2$\sqrt{5}$
=2$\sqrt{5}$-2$\sqrt{5}$+6+3
=9
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.$\sqrt{(-2)^{2}}$的值等于( )
| A. | -2 | B. | 2或-2 | C. | 4 | D. | 2 |
1.水龙头关闭不严会造成漏水,通过一次调查发现漏水量与漏水时间的关系如表:
漏水量与漏水时间近似于正比例函数关系,以表中每间隔5分钟漏水量的众数为依据,来估算这种漏水状态下一天该水龙头的漏水量.
| 时间 (分钟) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 水量 (毫升) | 0 | 21 | 41 | 59 | 79 | 101 | 121 |
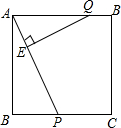 如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.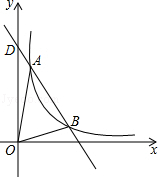 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.