题目内容
10.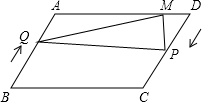 已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).
已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).(1)当PQ⊥PM时,求t的值;
(2)设△PCM的面积为y(cm2),求y与x之间的函数关系式;
(3)是否存在某一时刻使得△PQM的面积最大?若存在,求出此时t的值,并求出最大面积,若不存在,请说明理由;
(4)过点M作MN∥AB交BC于点N,连接PN,是否存在某一时刻使得PM=PN?若存在,求出此时t的值,若不存在,请说明理由.
分析 (1)只要证明四边形AQPD是平行四边形,得AQ=PD,列出方程即可解决问题.
(2)如图1中,作MN⊥CD于N,只要求出MN,根据y=$\frac{1}{2}$•PC•MN计算即可.
(3)如图2中,作BG⊥DA交DA的延长线于G,过点Q作QK⊥PM于K,交BG于H,求出QK,PM,构建二次函数,理由二次函数的性质即可解决问题.
(4)存在,只要证明CN=PC,根据PC+PD=CD列出方程即可解决问题.
解答 解:(1)∵PM⊥AD,PQ⊥PM,
∴PQ∥AD,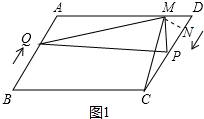
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴四边形AQPD是平行四边形,
∴AQ=PD,
∴20-2t=3t,
∴t=4.
(2)如图1中,作MN⊥CD于N,
在 RT△PMD中,∵∠PMD=90°,∠D=60°PD=3t,
∴DM=$\frac{1}{2}$PD=$\frac{3}{2}t$,
在RT△MND中,∵∠D=60°,∠MND=90°,
∴∠NMD=30°
∴DN=$\frac{1}{2}$DM=$\frac{3}{4}$t,MN=$\sqrt{3}$DN=$\frac{3\sqrt{3}}{4}$t,
当0<t≤$\frac{20}{3}$时,y=$\frac{1}{2}$•PC•MN=$\frac{1}{2}$(20-3t)•$\frac{3\sqrt{3}}{4}$t=-$\frac{9\sqrt{3}}{8}$t2+$\frac{15\sqrt{3}}{2}$.
当$\frac{20}{3}$<t≤10时,y=$\frac{1}{2}$•PC•NM=$\frac{1}{2}$(3t-20)•$\frac{3\sqrt{3}}{4}$t=$\frac{9\sqrt{3}}{8}$t2-$\frac{15\sqrt{3}}{2}$.
(3)如图2中,作BG⊥DA交DA的延长线于G,过点Q作QK⊥PM于K,交BG于H,则四边形GHKM是矩形,
在RT△ABG中,∵∠G=90°,∠ABG=30°,AB=20,
,∴AG=$\frac{1}{2}$AB=10,
在RT△BHQ中,∵∠BHQ=90°,∠HBQ=30°,BQ=2t,
∴HQ=$\frac{1}{2}$BQ=t,
∴QK=40-$\frac{3}{2}$t-t,
∴S△QPM=$\frac{1}{2}$•PM•QK=$\frac{1}{2}$×$\frac{3\sqrt{3}}{2}$t×(40-$\frac{5}{2}$t)=-$\frac{15\sqrt{3}}{8}$t2+30$\sqrt{3}$t,
∵a=-$\frac{15\sqrt{3}}{8}$<0,
∴S△QPM有最大值,此时t=-$\frac{30\sqrt{3}}{2×(-\frac{15\sqrt{3}}{8})}$=8,
∴t=8秒时,△QPM面积最大.
(4)存在.
理由:如图3中,∵PM=PN,
∴∠PMN=∠PNM,
∵AB∥MN,AM∥BN,
∴四边形ABNM是平行四边形,
∴∠AMN=∠MNC=∠B=60°,
∵∠PMD=90°,∠NMD=120°,
∴∠PMN=∠PNM=∠PNC=30°,
∵∠C=120°,
∴∠CPN=30°=∠PNC,
∴NC=PC=DM=$\frac{3}{2}$t,
∴PC+DP=20,
∴$\frac{3}{2}$t+3t=20,
∴t=$\frac{40}{9}$.
∴t=$\frac{40}{9}$s时,PM=PN.
点评 本题考查四边形综合题、平行四边形的性质、直角三角形30度角所对的直角边等于斜边的一半、勾股定理、三角形面积公式等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形利用勾股定理解决问题,属于中考压轴题.

| 时间 (分钟) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 水量 (毫升) | 0 | 21 | 41 | 59 | 79 | 101 | 121 |
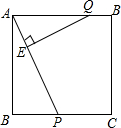 如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
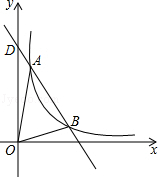 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.