题目内容
6.若反比例函数y=$\frac{k}{x}$的图象过点(-3,1),则该图象还经过( )| A. | (1,3) | B. | (3,-1) | C. | (3,1) | D. | (-1,-3) |
分析 根据反比例函数图象上点的坐标特征,可知反比例函数图象上任意一点其横坐标与纵坐标的乘积都等于比例系数k.先根据反比例函数y=$\frac{k}{x}$的图象过点(-3,1),求出k的值,再检验四个选项中的点,其横坐标与纵坐标的乘积是否等于k即可.
解答 解:∵反比例函数y=$\frac{k}{x}$的图象过点(-3,1),
∴k=-3×1=-3.
A、∵1×3=3≠-3,∴该图象不经过(1,3),故本选项不符合题意;
B、∵3×(-1)=-3,∴该图象经过(3,-1),故本选项符合题意;
C、∵3×1=3≠-3,∴该图象不经过(3,1),故本选项不符合题意;
D、∵-1×(-3)=3≠-3,∴该图象不经过(-1,-3),故本选项不符合题意;
故选B.
点评 本题考查了反比例函数图象上点的坐标特征,函数图象上的点一定满足函数的解析式;反之,满足函数的解析式的点一定在函数的图象上.

练习册系列答案
相关题目
16.计算:($\frac{1}{2}$)-1-(π-1)0,结果正确的是( )
| A. | 2 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
1.水龙头关闭不严会造成漏水,通过一次调查发现漏水量与漏水时间的关系如表:
漏水量与漏水时间近似于正比例函数关系,以表中每间隔5分钟漏水量的众数为依据,来估算这种漏水状态下一天该水龙头的漏水量.
| 时间 (分钟) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 水量 (毫升) | 0 | 21 | 41 | 59 | 79 | 101 | 121 |
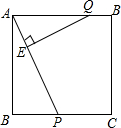 如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.