题目内容
14.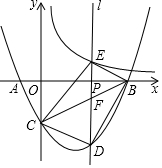 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.(1)求a,b的值;
(2)设点P的横坐标为m,四边形CDBE的面积为S,求S与m的函数关系式,并写出m的取值范围;
(3)在(2)中的条件下,是否存在m值,使四边形CDBE是平行四边形,若存在,请求出m值,若不存在,请说明理由.
分析 (1)理由待定系数法即可解决问题;
(2)根据四边形CDBE的面积S=S△DEC+S△DEB=$\frac{1}{2}$DE•CH+$\frac{1}{2}$DE•BP=$\frac{1}{2}$DE•(CH+BP),求解即可;
(3)存在.m=4满足题目条件.假设F是BC中点,证明EF=DF即可解决问题;
解答 解:(1)将A、B两点坐标代入y=ax2+bx-4得到,
$\left\{\begin{array}{l}{4a-2b-4=0}\\{64a+8b-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$.
(2)由(1)得y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4,作CH⊥y轴于点H,
∵P(m,0),可得E(m,$\frac{8}{m}$),D(m,$\frac{1}{4}$m2-$\frac{3}{2}$m-4),
∴CH=m,DE=$\frac{8}{m}$-$\frac{1}{4}$m2+$\frac{3}{2}$m+4,BP=8-m,
∴四边形CDBE的面积S=S△DEC+S△DEB=$\frac{1}{2}$DE•CH+$\frac{1}{2}$DE•BP=$\frac{1}{2}$DE•(CH+BP)=-m2+6m+$\frac{32}{m}$+16(0<m<8).
(3)存在.m=4满足题目条件.
理由:当F为BC中点时,根据三角形中位线定理,可知F(4,-2),
∴m=4,即点P坐标为(4,0),
∴把x=4代入y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4,求得y=-6,
把x=4代入y=$\frac{8}{x}$,求得y=2,
∴D(4,-6),E(4,2),
∴EF=2-(-2)=4,DF=-2-(6)=4,
∴EF=DF,
∴当F为BC中点时,四边形CDBE是平行四边形,
∴存在m=4时,四边形CDBE是平行四边形.
点评 本题考查二次函数综合题、反比例函数的性质、四边形的面积、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案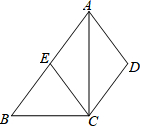 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.如果点E是AB的中点,AC=4,EC=2.5,写出求四边形ABCD的面积的思路.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.如果点E是AB的中点,AC=4,EC=2.5,写出求四边形ABCD的面积的思路. 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,AF=EC,求证:四边形EBFD是平行四边形.
如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,AF=EC,求证:四边形EBFD是平行四边形.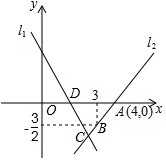 如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.
如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.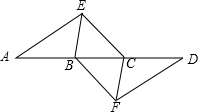 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.