题目内容
4.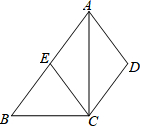 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.如果点E是AB的中点,AC=4,EC=2.5,写出求四边形ABCD的面积的思路.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.如果点E是AB的中点,AC=4,EC=2.5,写出求四边形ABCD的面积的思路.
分析 由条件可证明四边形AECD为平行四边形,结合角平分线的定义可求得AE=CE,可证得四边形AECD为菱形,进一步可证得△ABC为直角三角形,则可求得△AEC、△ADC和△BEC的面积,可求得四边形ABCD的面积.
解答 解:
①由AD∥CE,AE∥CD,可得四边形AECD为平行四边形,
②由AC平分∠BAD,AD∥CE,可得AE=CE,
综合①②可得四边形AECD是菱形,
③由∠ACE=∠EAC,∠ECB=∠B和△ABC内角和180°,可得△ABC是直角三角形,
④由菱形AECD和E为中点,可得S△AEC=S△ACD=S△BEC=3,
∴四边形ABCD的面积为9.
点评 本题主要考查菱形的判定和性质,先证得四边形AECD为菱形是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
15.有两根长分别是20厘米和30厘米的木棒,若不改变木棒的长度,要钉成一个三角形框架,则应在下列木棒中选取( )厘米的木棒.
| A. | 10 | B. | 20 | C. | 50 | D. | 60 |
 如图,已知线段a,b,∠α(如图).
如图,已知线段a,b,∠α(如图).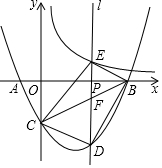 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.