题目内容
3.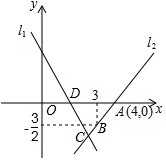 如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.
如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.
分析 联立两直线表达式成方程组,解方程组即可得出点C的坐标,根据一次函数图象上点的坐标特征可得出点D的坐标,再根据三角形的面积公式,即可求出△ADC的面积.
解答 解:联立两直线表达式成方程组,
$\left\{\begin{array}{l}{y=-3x+3}\\{y=\frac{3}{2}x-6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴点C的坐标为(2,-3).
当y=-3x+3=0时,x=1,
∴点D的坐标为(1,0),
∴S△ADC=$\frac{1}{2}$AD•|yC|=$\frac{1}{2}$×(4-1)×3=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了一次函数图象上点的坐标特征、两直线相交或平行问题以及三角形的面积,根据一次函数图象上点的坐标特征以及解方程组求出点C、D的坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.南京为建设绿色之都,计划在路旁栽树1200棵,由于志愿者的参与,实际每天栽树的棵数比计划多栽了20%,结果提前2天完成任务.设原计划每天栽x棵树.
(1)根据条件填表:
(2)求原计划每天栽树多少棵?
(1)根据条件填表:
| 工作总量 | 工作时间 | 工作效率 | |
| 计划 | 1200 | $\frac{1200}{x}$ | x |
| 实际 | 1200 | $\frac{1200}{1.2x}$ | 1.2x |
1.如果A=-x2+4x-1,B=-x2-4x+1,那么B-A等于 ( )
| A. | -2x2 | B. | 8x-2 | C. | 2-8x | D. | 0 |
 如图,已知线段a,b,∠α(如图).
如图,已知线段a,b,∠α(如图).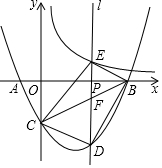 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
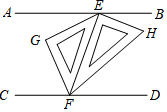 已知:如图,AB∥CD,一副三角板按如图所示放置,∠AEG=30°.求∠HFD的度数.
已知:如图,AB∥CD,一副三角板按如图所示放置,∠AEG=30°.求∠HFD的度数. 某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.