题目内容
4.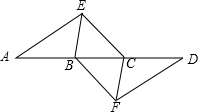 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;
(2)若AD=8,DC=3,∠EBD=60°,当四边形BFCE是菱形时,求BE的长.
分析 (1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
解答 (1)证明:∵AB=DC,
∴AC=DB,
在△AEC和△DFB中,
$\left\{\begin{array}{l}{AC=DB}\\{∠A=∠D}\\{AE=DF}\end{array}\right.$,
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF,
∴EC∥BF,
∴四边形BFCE是平行四边形;
(2)解:当四边形BFCE是菱形时,BE=CE,
∵AD=8,DC=3,AB=CD=3,
∴BC=8-3-3=2,
∵∠EBD=60°,
∴BE=BC=2,
∴当四边形BFCE是菱形时,BE的长是2.
点评 此题考查了全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质等知识.此题综合性较强,难度适中,注意数形结合思想的应用,注意掌握辅助线的作法.

练习册系列答案
相关题目
12.南京为建设绿色之都,计划在路旁栽树1200棵,由于志愿者的参与,实际每天栽树的棵数比计划多栽了20%,结果提前2天完成任务.设原计划每天栽x棵树.
(1)根据条件填表:
(2)求原计划每天栽树多少棵?
(1)根据条件填表:
| 工作总量 | 工作时间 | 工作效率 | |
| 计划 | 1200 | $\frac{1200}{x}$ | x |
| 实际 | 1200 | $\frac{1200}{1.2x}$ | 1.2x |
1.如果A=-x2+4x-1,B=-x2-4x+1,那么B-A等于 ( )
| A. | -2x2 | B. | 8x-2 | C. | 2-8x | D. | 0 |
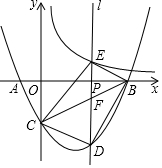 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D. 某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示. 用长为6m的铝合金制成如图窗框,窗框的上部为由两个正方形组成的矩形,解答下列问题:
用长为6m的铝合金制成如图窗框,窗框的上部为由两个正方形组成的矩形,解答下列问题: 如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.
如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.