题目内容
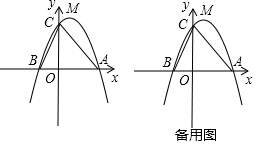
2.一次函数y=-2x+4与x轴、y轴分别交于点A、B,点C与点A关于y轴对称.(1)求△ABC的面积;
(2)m为实数,判断点P(m+2,-2m+1)是否在该函数的图象上,并说明理由.
分析 (1)根据一次函数图象上点的坐标特征可求出点A、B的坐标,由点C与点A关于y轴对称可得出点C的坐标,再根据三角形的面积公式可求出△ABC的面积;
(2)将x=m+2代入一次函数解析式中求出y值,对比后即可得知点P在不在函数的图象上.
解答 解:(1)当x=0时,y=-2x+4=4,
∴点B的坐标为(0,4);
当y=-2x+4=0时,x=2,
∴点A的坐标为(2,0).
∵点C与点A关于y轴对称,
∴点C的坐标为(-2,0),
∴S△ABC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×[2-(-2)]×4=8.
(2)当x=m+2时,y=-2(m+2)+4=-2m≠-2m+1,
∴点P不在该函数的图象上.
点评 本题考查了一次函数图象上点的坐标特征、关于x轴、y轴对称的点的坐标以及三角形的面积,解题的关键是:(1)根据一次函数图象上点的坐标特征求出点A、B的坐标是解题的关键;(2)将x=m+2代入一次函数解析式中求出y值.

练习册系列答案
相关题目
12.南京为建设绿色之都,计划在路旁栽树1200棵,由于志愿者的参与,实际每天栽树的棵数比计划多栽了20%,结果提前2天完成任务.设原计划每天栽x棵树.
(1)根据条件填表:
(2)求原计划每天栽树多少棵?
(1)根据条件填表:
| 工作总量 | 工作时间 | 工作效率 | |
| 计划 | 1200 | $\frac{1200}{x}$ | x |
| 实际 | 1200 | $\frac{1200}{1.2x}$ | 1.2x |
 如图,已知线段a,b,∠α(如图).
如图,已知线段a,b,∠α(如图).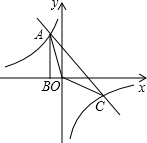 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$,求:
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$,求: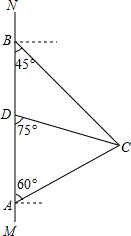 如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
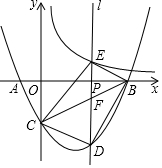 如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.
如图,抛物线y=ax2+bx-4与x轴交于A(-2,0)、B(8,0)两点(B在A的右侧),与y轴交于点C,点P是线段OB的一个动点(点P不与O、B重合),过点P作直线l⊥x轴,交双曲线y=$\frac{8}{x}$(x>0)于点E,交线段BC于点F,交抛物线于点D.