题目内容
6.正六边形的两条对边之间的距离是2$\sqrt{3}$,则它的边长是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 画出图形,根据题意求出MN=2$\sqrt{3}$,解直角三角形求出AM,即可求出答案.
解答 解:
连接OA、OB,设MN⊥AB、MN⊥DE,MN过中心O,
∵ABCDEF是正六边形,
∴∠AOB=60°,∠AOM=30°,
∵正六边形的两条对边之间的距离是2$\sqrt{3}$,
∴OM=ON=$\sqrt{3}$,
∴AM=OM×tan∠AOM=1,
∵OA=OB,OM⊥AB,
∴AB=2AM=2,
故选B.
点评 本题考查了正多边形和圆、解直角三角形、等腰三角形的性质等知识点,能综合运用知识点进行计算和推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.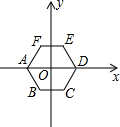 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )| A. | (1,-2) | B. | (1,-$\sqrt{2}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
17.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的个数有( )
①ab<0②a+b>0③a2>b2④a<-b<b<-a
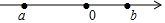
①ab<0②a+b>0③a2>b2④a<-b<b<-a
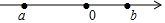
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
 如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )| A. | $\frac{2}{5}$$\sqrt{5}$ | B. | $\frac{1}{2}$$\sqrt{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{4}$$\sqrt{13}$ |
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB的度数为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB的度数为( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB的度数为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
11.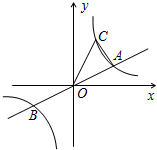 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=$\frac{k}{x}$(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )| A. | (2,4) | B. | (1,8) | C. | (2,4)或(1,8) | D. | (2,4)或(8,1) |
15.在同一时刻,身高1.8m的小强影长是1.2m,旗杆的影长是15m,则旗杆高为( )
| A. | 22.5m | B. | 24m | C. | 20.5m | D. | 10m |
16.sin60°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
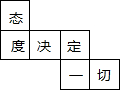 小李同学的座右铭是“态度决定一切“,他将这几个字写在一个正方体纸盒的每个面上,其平面展开图如图所示,那么在该正方体中,和“切”相对的字是( )
小李同学的座右铭是“态度决定一切“,他将这几个字写在一个正方体纸盒的每个面上,其平面展开图如图所示,那么在该正方体中,和“切”相对的字是( )