题目内容
9.三角形的边长之比为:①1.5:2:2.5;②4:7.5:8.5;③1:$\sqrt{3}$:2;④3.5:4.5:5.5.其中可以构成直角三角形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 判断是否为直角三角形,这里给出三边的长,只要验证两小边的平方和是否等于最长边的平方即可.
解答 解:①1.52+22=2.52,能构成直角三角形,故正确;
②42+7.52=8.52,能构成直角三角形,故正确;
③12+$\sqrt{3}$2=22,能构成直角三角形,故正确;
④3.52+4.52≠5.52,不能构成直角三角形,故错误.
故选C.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
19.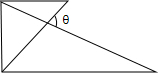 将一副三角板按如图方式叠放,则角θ为( )
将一副三角板按如图方式叠放,则角θ为( )
 将一副三角板按如图方式叠放,则角θ为( )
将一副三角板按如图方式叠放,则角θ为( )| A. | 75度 | B. | 60度 | C. | 45度 | D. | 30度 |
4.把抛物线y=-x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x+3)2+1 | B. | y=-(x+1)2+3 | C. | y=-(x-1)2+4 | D. | y=-(x+1)2+4 |
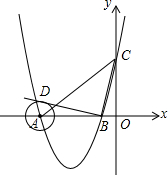 如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).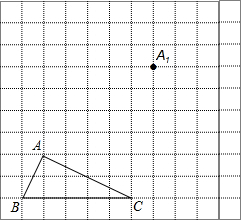 如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上).
如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上).