题目内容
18.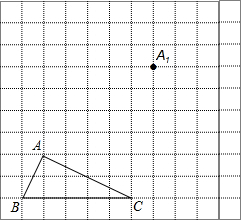 如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上).
如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上).(1)平移△ABC,使得点A移到A1的位置,在网格中画出平移后得到的△A1B1C1;
(2)把(1)中的△A1B1C1绕点A1按顺时针方向旋转90°,在网格中画出旋转后得到的△A1B2C2;
(3)如果网格中小正方形的边长为1,点C经过(1)、(2)变换路径总长度为$\sqrt{41}$+5π.
分析 (1)利用平移的性质画图,即对应点都移动相同的距离;
(2)利用旋转的性质画图,对应点都旋转相同的角度;
(3)利用弧长公式求点B经过(1)、(2)变换的路径总长.
解答 解:(1)如图所示:
(2)画图如下:
(3)C经过(1)、(2)变换的路径如图红色部分所示:
CC1=$\sqrt{{5}^{2}+{4}^{2}}$=$\sqrt{41}$,
弧C1C2的长=$\frac{90π×({2}^{2}+{4}^{2})}{360}$=5π,
故点C所走的路径总长=$\sqrt{41}$+5π.
故答案是:$\sqrt{41}$+5π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
相关题目
13.若-5是一元二次方程x2-9x+m=0的一个根,则方程的另一根是( )
| A. | 4 | B. | -4 | C. | 14 | D. | -14 |
3.下列命题中,是真命题的有( )
①若a>b,则ac>bc;
②$\sqrt{25}$的平方根是±5;
③函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y)一定在第二象限;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5.
①若a>b,则ac>bc;
②$\sqrt{25}$的平方根是±5;
③函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y)一定在第二象限;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.2015年4月某日我市区县的可吸入颗粒物数值统计如下表:
该日这一时刻的可吸入颗粒物数值的众数和中位数分别是( )
| 区县 | 宣威 | 富源 | 沾益 | 马龙 | 师宗 | 罗平 | 陆良 | 会泽 | 麒麟区 | 经开区 |
| 可吸入颗粒物 (mg/m3) | 0.18 | 0.18 | 0.15 | 0.13 | 0.14 | 0.13 | 0.15 | 0.15 | 0.15 | 0.14 |
| A. | 0.15和0.14 | B. | 0.18和0.15 | C. | 0.18和0.14 | D. | 0.15和0.15 |
 如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处24米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,求旗杆的高CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】
如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处24米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,求旗杆的高CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】