题目内容
6.(1)我们把顶点在正方形网格格点上的三角形称为格点三角形.在7×4的网格中,格点△ABC和格点△DEF如图①所示.①试说明:△ABC∽△DEF;②求∠B+∠D的度数;
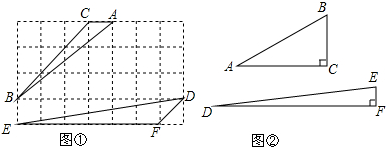
(2)图②中,已知△ABC和△DEF中,∠C=∠F=90°,AC=m,BC=n,其中m>n,则$\frac{DF}{EF}$为多少时(用m、n的代数式表示),∠A+∠D的度数为45°?请说明理由.
分析 (1)①根据勾股定理分别求出两个三角形的边长,根据相似三角形的判定定理证明即可;
②根据相似三角形的性质得到∠B=∠E,等量代换即可;
(2)在CA上截取CM=CB=n,连接BM,作MN⊥AB于N,根据勾股定理求出$\frac{BM}{MN}$,证明△EFD∽△MNB,根据相似三角形的性质定理解答即可.
解答 解:(1)①AC=1,BC=3$\sqrt{2}$,AB=5,
DF=$\sqrt{2}$,EF=6,DE=5$\sqrt{2}$,
则$\frac{AC}{DF}$=$\frac{\sqrt{2}}{2}$,$\frac{BC}{EF}$=$\frac{\sqrt{2}}{2}$,$\frac{AB}{DE}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AC}{DF}$=$\frac{BC}{EF}$=$\frac{AB}{DE}$,
∴△ABC∽△DEF;
②∵△ABC∽△DEF;
∴∠B=∠E,
又∠E+∠D=45°,
∴∠B+∠D=45°;
(2)如图,在CA上截取CM=CB=n,连接BM,作MN⊥AB于N,
则∠CMB=∠CBM=45°,BM=$\sqrt{2}$n,
∴∠A+∠ABM=45°,
∵∠C=90°,AC=m,BC=n,
∴AB=$\sqrt{{m}^{2}+{n}^{2}}$,
∴$\frac{1}{2}$×AB×MN=$\frac{1}{2}$×AM×BC,即$\sqrt{{m}^{2}+{n}^{2}}$×MN=(m-n)×n,
解得,MN=$\frac{n(m-n)}{\sqrt{{m}^{2}+{n}^{2}}}$,
∴$\frac{BM}{MN}$=$\sqrt{2}$n×$\frac{\sqrt{{m}^{2}+{n}^{2}}}{n(m-n)}$=$\frac{\sqrt{2{m}^{2}+2{n}^{2}}}{m-n}$,
∵∠A+∠D=45°,∠A+∠ABM=45°,
∴∠D=∠ABM,又∠MNB=∠F=90°,
∴△EFD∽△MNB,
∴$\frac{DE}{EF}$=$\frac{BM}{MN}$=$\frac{\sqrt{2{m}^{2}+2{n}^{2}}}{m-n}$.
点评 本题考查的是相似三角形的判定和性质、勾股定理的应用,掌握相似三角形的判定定理和性质定理是解题的关键.

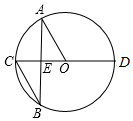 如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )
如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )| A. | 120° | B. | 100° | C. | 170° | D. | 150° |
 有理数a、b在数轴上的位置如图所示,则a+b的值是( )
有理数a、b在数轴上的位置如图所示,则a+b的值是( )| A. | 正数 | B. | 负数 | C. | 零 | D. | 符号不确定 |
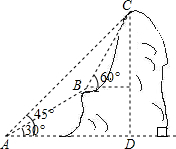 如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)? 如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.
如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.