题目内容
15.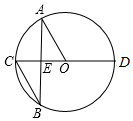 如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )
如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为( )| A. | 120° | B. | 100° | C. | 170° | D. | 150° |
分析 首先根据∠BAO=30°,AO∥BC利用两直线平行,内错角相等求得∠ABC的度数,然后利用圆周角定理求得∠AOC的度数,从而利用邻补角的定义求得∠AOD的度数.
解答 解:∵∠BAO=30°,AO∥BC,
∴∠ABC=30°,
∴∠AOC=60°,
∴∠AOD=180°-∠AOC=180°-60°=120°,
故选A.
点评 本题考查了圆周角定理的知识,解题的关键是能够从图中找到同弧所对的圆周角及圆心角,难度不大.

练习册系列答案
相关题目
5. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,若∠A=40°,则∠C等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 50° |
7.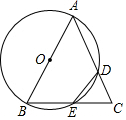 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
5.已知点M(a,2),点N(3,b)关于y轴对称,则(a+b)2016=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
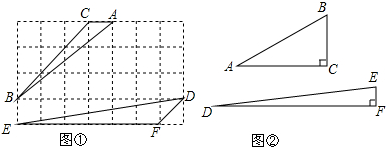
 如图:
如图: