题目内容
17．
如图所示，分别以n边形顶角顶点为圆心，以1cm长为半径画圆，则圆中阴影部分面积之和为πcm2．
分析 由于多边形的外角和为360°，则所有阴影的扇形的圆心角的和为360度，故阴影部分的面积即可求得．
解答 解：∵多边形的外角和为360°，
∴SA1+SA2+…+SAn=S圆=π×12=π（cm2）．
故答案为πcm2．
点评 本题考查了圆的面积公式的应用，多边形的外角和定理，扇形的面积计算，关键是正确找出阴影部分面积的计算方法．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
5．
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，若∠A=40°，则∠C等于（ ）
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，若∠A=40°，则∠C等于（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 50° |
12．如表，从左到右在每个小格子中填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等
（1）可求得c=1，第2016个格子中的数为-4
（2）前m个格子中所填整数之和是否可能为2016？若能，求m的值；若不能，请说明理由
（3）数轴上，点A、点B对应的数分别是a、b，在数轴上是否存在点P，使得|PA|+|PB|=15？求出P点对应的数（说明：|PA|表示P到A点的距离）
| 1 | a | b | c | 8 | -4 | … |
（2）前m个格子中所填整数之和是否可能为2016？若能，求m的值；若不能，请说明理由
（3）数轴上，点A、点B对应的数分别是a、b，在数轴上是否存在点P，使得|PA|+|PB|=15？求出P点对应的数（说明：|PA|表示P到A点的距离）
如图，AB∥CD，∠E=65°，则∠B+∠F+∠C=245°．
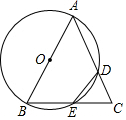如图，在△ABC中，AB=AC，以AB为直径的圆分别交边AC，BC于点D，E，若$\widehat{AD}$=$\widehat{DE}$+30°，则∠DEC的度数是（ ）