题目内容
8.用适当的方法解方程:(1)(x-1)(x+2)=6.
(2)x2=2x+35.
分析 (1)先把方程化为一般式,然后利用求根公式法解方程;
(2)先把方程化为一般式,然后利用因式分解法解方程.
解答 解:(1)x2+x-8=0,
△=b2-4ac=1+32=33>0,
∴x=$\frac{-1±\sqrt{33}}{2}$,
∴x1=$\frac{-1+\sqrt{33}}{2}$,x2=$\frac{-1-\sqrt{33}}{2}$;
(2)移项得:x2-2x-35=0,
(x-7)(x+5)=0,
x-7=0或x+5=0,
所以x1=7,x2=-5.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
19.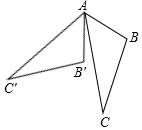 如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )
如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )
 如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )
如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )| A. | 22° | B. | 23° | C. | 24° | D. | 25° |
17.如表是某次篮球联赛积分的一部分
(1)请问胜一场积多少分?负一场积多少分?
(2)某队的负场总积分是胜场总积分的n倍,n为正整数,求n的值.
(注意:本题只能用一元一次方程求解,否则不给分).
| 球队 | 比赛现场 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
| 备注:积分=胜场积分+负场积分 | ||||
(2)某队的负场总积分是胜场总积分的n倍,n为正整数,求n的值.
(注意:本题只能用一元一次方程求解,否则不给分).
18.下列各式中,正确的是( )
| A. | -(2x+5)=2x+5 | B. | -$\frac{1}{2}$(4x-2)=-2x+2 | C. | -a+b=-(a-b) | D. | 2-3x=(3x+2) |
 如图,在△ABC中,D、E分别是AC、AB边上的点,∠AED=∠C,AB=10,AD=6,AC=8,求BE的长.
如图,在△ABC中,D、E分别是AC、AB边上的点,∠AED=∠C,AB=10,AD=6,AC=8,求BE的长.