题目内容
19．
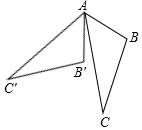如图所示，△ABC中，∠BAC=32°，将△ABC绕点A按顺时针方向旋转55°，对应得到△AB′C′，则∠B′AC的度数为（ ）| A． | 22° | B． | 23° | C． | 24° | D． | 25° |
分析 先利用旋转的性质得到∠B'AC'=32°，∠BAB'=55°，从而得到∠B′AC的度数．
解答 解：∵∠BAC=32°，将△ABC绕点A按顺时针方向旋转55°，对应得到△AB′C′，
∴∠B'AC'=32°，∠BAB'=55°，
∴∠B′AC的度数=55°-32°=23°．
根本B．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
相关题目
9．某班男生有x人，女生人数占全班人数的45%，则该班女生人数是（ ）人．
| A． | 45%x | B． | 45%+x | C． | $\frac{x}{45%}$-x | D． | $\frac{x}{1-45%}$-x |
10．方程x2+4x-4=0 经过配方后，其结果正确的是（ ）
| A． | （x+2）2=4 | B． | （x-2）2=4 | C． | （x-2）2=8 | D． | （x+2）2=8 |
7．下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（ ）
| A． | 用两个钉子就可以把木条固定在墙上 | |
| B． | 利用圆规可以比较两条线段的大小关系 | |
| C． | 把弯曲的公路改直，就能缩短路程 | |
| D． | 植树时，只要定出两棵树的位置，就能确定同一行树所在的直线 |
14．
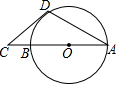如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=40°，则∠CDA的度数是（ ）
如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=40°，则∠CDA的度数是（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
已知：如图，在△ABC中，点D、E分别在边AB，AC上，且∠AED=∠ABC，DE=3，BC=5，AC=12．求AD的长．