题目内容
13.解方程:(1)x2-5=4x
(2)x2+2x-5=0.
分析 (1)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)移项得:x2-4x-5=0,
(x-5)(x+1)=0,
∴x-5=0,x+1=0,
∴x1=5,x2=-1;
(2)x2+2x-5=0,
x2+2x=5,
x2+2x+1=5+1,
(x+1)2=6,
x+1=±$\sqrt{6}$,
x1=$\sqrt{6}$-1,x2=-$\sqrt{6}$-1.
点评 本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
4.在摸球实验中,暗盒内装有8个白色乒乓球和若干个黄色乒乓球,某同学进行如下试验:每次任意摸出1个球,记下颜色后放回并搅匀,再任意摸出1个球,如此重复多次试验后,得到摸出白球的频率是0.25,根据上述数据可估计盒子中黄球的个数为( )
| A. | 16个 | B. | 24个 | C. | 32个 | D. | 40个 |
2. 如图所示,在数轴上表示|-3|的点是( )
如图所示,在数轴上表示|-3|的点是( )
 如图所示,在数轴上表示|-3|的点是( )
如图所示,在数轴上表示|-3|的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
3. 如图,在?ABCD中,点E、F分别在边AD、CD上,连接BE、AF,它们相交于点G,BE的延长线与CD的延长线相交于点H,下列结论中正确的是( )
如图,在?ABCD中,点E、F分别在边AD、CD上,连接BE、AF,它们相交于点G,BE的延长线与CD的延长线相交于点H,下列结论中正确的是( )
 如图,在?ABCD中,点E、F分别在边AD、CD上,连接BE、AF,它们相交于点G,BE的延长线与CD的延长线相交于点H,下列结论中正确的是( )
如图,在?ABCD中,点E、F分别在边AD、CD上,连接BE、AF,它们相交于点G,BE的延长线与CD的延长线相交于点H,下列结论中正确的是( )| A. | $\frac{EG}{BG}$=$\frac{AE}{BC}$ | B. | $\frac{EH}{EB}$=$\frac{DH}{CH}$ | C. | $\frac{AE}{ED}$=$\frac{BE}{EH}$ | D. | $\frac{AG}{FG}$=$\frac{BG}{FH}$ |
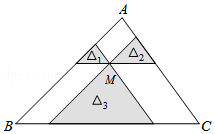 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.