Question

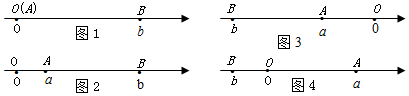
19．（1）阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．
当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|；
当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
②如图3，点A、B都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
③如图4，点A、B在原点的两边，|AB|=|OB|+|OA|=|a|+|b|=a+（-b）=|a-b|；

（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是3；
数轴上表示-2和-5的两点之间的距离是3；
数轴上表示1和-3的两点之间的距离是4；
②数轴上表示x和-1的两点A和B之间的距离是|x+1|，如果|AB|=2，那么x为-3或1；
③请你找出所有符合条件的整数x，使代数式|x+1|+|x-2|=3，这样的整数是-1，0，1，2．

Answer 1

分析 （2）①根据两点之间的距离公式即可求解；
②在数轴上，某点到-1所对应的点的距离为2；
③利用数轴解决：把|x+1|+|x-2|=3理解为：在数轴上，某点到-1所对应的点的距离和到2所对应的点的距离之和为3，然后根据数轴可写出满足条件的整数即可．

解答 解：（2）①数轴上表示2和5的两点之间的距离是5-2=3；
数轴上表示-2和-5的两点之间的距离是-2-（-5）=3；
数轴上表示1和-3的两点之间的距离是|1-（-3）|=4；

②数轴上表示x和-1的两点A和B之间的距离是|x-（-1）|=|x+1|，
|AB|=2，可理解为：在数轴上，某点到-1所对应的点的距离为2，则x=-3或1；
故答案是：7或-4；

③式子|x+1|+|x-2|=3可理解为：在数轴上，某点到-1所对应的点的距离和到2所对应的点的距离之和为3，
所以满足条件的整数可为-1，0，1，2．
故答案是：3，3，4；|x+1|，-3或1；-1，0，1，2．

点评 此题主要考查了去绝对值和数轴相联系的综合试题以及去绝对值的方法和去绝对值在数轴上的运用，难度较大，去绝对的关键是确定绝对值里面的数的正负性．