题目内容
 如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6).
如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6).(1)求直线AB的解析式;
(2)在线段AB上有一个点P,过点P分别作x、y轴的垂线,垂足分别为点E、F,若矩形OEPF的面积为9,求点P的坐标;
(3)在第一象限内是否存在点Q,使△QOB与△BOA相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法即可求得;
(2)设P的坐标为(x,-
x+6),根据矩形的面积公式即可求得;
(3)分四种情况分别讨论即可求得.
(2)设P的坐标为(x,-
| 3 |
| 4 |
(3)分四种情况分别讨论即可求得.
解答:解:(1)设直线AB的解析式为y=kx+b,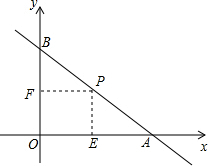
∵点A(8,0)、B(0,6),
∴
,
解得:
,
∴直线AB的解析式为y=-
x+6;
(2)设P的坐标为(x,-
x+6),
则S矩形OEPF=OE•OF=x•(-
x+6)=9,
解得:x1=2,x2=6,
∴点P(2,
)或(6,
);
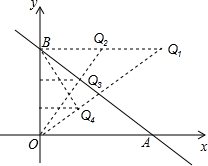 (3)①当△OBQ1∽△BOA时,则∠OBQ1=∠BOA=90°,
(3)①当△OBQ1∽△BOA时,则∠OBQ1=∠BOA=90°,
∴BQ1∥OA,BQ1=OA,
∴Q1(8,6),
②当△Q2BO∽△BOA时,则∠OBQ2=∠BOA=90°,
∴BQ2∥OA,
=
,
∴BQ2=
=
,
∴Q2(
,6);
③当△BQ3O∽△BOA时,则∠OBQ2=∠BOA=90°,∠OBQ3=∠AOB,
∴Q3在AB上,
=
,
∵OA=8,OB=6,
∴AB=
=10,
∴BQ3=
=
,
设Q3的坐标为(m,n)
∴
=
=
,解得,m=
,n=
,
∴Q3(
,
);
④当△OQ4B∽△BOA时,则∠OQ4B=∠BOA=90°,
作Q4的横坐标=Q3的横坐标=
,Q4的纵坐标=6-n=
;
∴Q4(
,
);
综上,Q点的坐标为(8,6)或(
,6)或(
,
)或(
,
).

∵点A(8,0)、B(0,6),
∴
|
解得:
|
∴直线AB的解析式为y=-
| 3 |
| 4 |
(2)设P的坐标为(x,-
| 3 |
| 4 |
则S矩形OEPF=OE•OF=x•(-
| 3 |
| 4 |
解得:x1=2,x2=6,
∴点P(2,
| 9 |
| 2 |
| 3 |
| 2 |
 (3)①当△OBQ1∽△BOA时,则∠OBQ1=∠BOA=90°,
(3)①当△OBQ1∽△BOA时,则∠OBQ1=∠BOA=90°,∴BQ1∥OA,BQ1=OA,
∴Q1(8,6),
②当△Q2BO∽△BOA时,则∠OBQ2=∠BOA=90°,
∴BQ2∥OA,
| BQ2 |
| OB |
| OB |
| OA |
∴BQ2=
| 6×6 |
| 8 |
| 9 |
| 2 |
∴Q2(
| 9 |
| 2 |
③当△BQ3O∽△BOA时,则∠OBQ2=∠BOA=90°,∠OBQ3=∠AOB,
∴Q3在AB上,
| BQ3 |
| OB |
| OB |
| AB |
∵OA=8,OB=6,
∴AB=
| OA2+OB2 |
∴BQ3=
| 6×6 |
| 10 |
| 18 |
| 5 |
设Q3的坐标为(m,n)
∴
| 6-n |
| 6 |
| m |
| 8 |
| ||
| 10 |
| 72 |
| 5 |
| 96 |
| 25 |
∴Q3(
| 72 |
| 25 |
| 96 |
| 25 |
④当△OQ4B∽△BOA时,则∠OQ4B=∠BOA=90°,
作Q4的横坐标=Q3的横坐标=
| 72 |
| 25 |
| 54 |
| 25 |
∴Q4(
| 72 |
| 25 |
| 54 |
| 25 |
综上,Q点的坐标为(8,6)或(
| 9 |
| 2 |
| 72 |
| 25 |
| 96 |
| 25 |
| 72 |
| 25 |
| 54 |
| 25 |
点评:本题考查了待定系数法求解析式,矩形的面积的求法,三角形相似的性质等;熟练掌握和运用性质是解题的关键.

练习册系列答案
相关题目
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论中错误的是( )
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论中错误的是( )| A、∠AGE=67.5° | ||
| B、四边形AEFG是菱形 | ||
| C、BE=2OF | ||
D、S△DOG:S四边形OGEF=
|
 下列是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,填空.
下列是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,填空.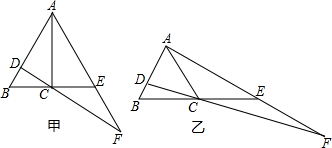
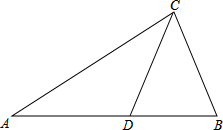
 已知如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ACB的平分线交AD于点E,求证:点E在∠ABC的平分线上.
已知如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ACB的平分线交AD于点E,求证:点E在∠ABC的平分线上. 已知正方形的边长为1,则图中阴影部分的面积为
已知正方形的边长为1,则图中阴影部分的面积为