Question

如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的F重合．展开后，折痕DE分别交AB，AC于点E，G．连接GF．下列结论中错误的是（　　）

• A、∠AGE=67.5°
• B、四边形AEFG是菱形
• C、BE=2OF
• D、S_△DOG：S_{四边形OGEF}=

  2

  ：1

Answer 1

考点：翻折变换（折叠问题）

专题：计算题

分析：根据正方形的性质得∠AOB=90°，∠BAO=∠OAD=∠ODA=45°，再根据折叠的性质得∠1=∠2=

1

2

∠ODA=22.5°，EA=EF，∠4=∠5，∠EFD=∠EAD=90°，于是根据三角形外角性质可计算出∠3=67.5°，即∠AGE=67.5°；根据三角形内角和可计算出∠4=67.5°，则∠3=∠4=∠5，所以AE=AG=EF，AG∥EF，于是可判断四边形AEFG为菱形；根据菱形性质得GF∥AB，EF=GF，利用平行线性质得∠6=∠7=45°，则可判断△BEF和△OGF都是等腰直角三角形，得到BE=

2

EF，GF=

2

OF，所以BE=2OF；设OF=a，则GF=

2

a，BF=

2

a，可计算出OB=（

2

+1）a，则OD=（

2

+1）a，DF=DO+OF=（2+

2

）a，再证明△DOG∽△DFE，利用相似三角形的性质可计算出

S△DOG

S△DFE

=（

DO

DF

）²=

1

2

，则S_△DOG：S_{四边形OGEF}=1：1，即D选项的结论错误．

解答：解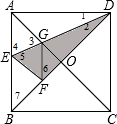：∵四边形ABCD为正方形，
∴∠AOB=90°，∠BAO=∠OAD=∠ODA=45°，
∵折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的F重合，
∴∠1=∠2=

1

2

∠ODA=22.5°，EA=EF，∠4=∠5，∠EFD=∠EAD=90°，
∴∠3=∠GAD+∠1=45°+22.5°=67.5°，即∠AGE=67.5°；
∵∠4=90°-∠1=67.5°，
∴∠3=∠4=∠5，
∴AE=AG=EF，AG∥EF，
∴四边形AEFG为菱形；
∴GF∥AB，EF=GF，
∴∠6=∠7=45°，
∴△BEF和△OGF都是等腰直角三角形，
∴BE=

2

EF，GF=

2

OF，
∴BE=

2

•

2

OF=2OF；
设OF=a，则GF=

2

a，BF=

2

a，
∴OB=（

2

+1）a，
∴OD=（

2

+1）a，DF=DO+OF=（2+

2

）a，
∵∠DOG=∠DFE=90°，
∴△DOG∽△DFE，
∴

S△DOG

S△DFE

=（

DO

DF

）²=[

( 2 +1)a

(2+ 2 )a

]²=

1

2

，
∴S_△DOG：S_{四边形OGEF}=1：1．
故选D．

点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了正方形和等腰直角三角形的性质．