题目内容
王晓说:有一个三角形(记为△ABC),其中∠B=60°,D是AB上一点,连接CD,延长BC至点E,使CE=BC,连接AE并延长,交DC的延长线于点F.爸爸,您能根据我上面的描述用AuToCAD画出来吗?
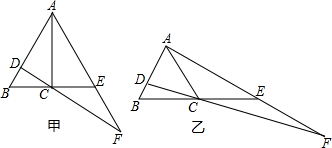
爸爸说:当然!我根据你的描述画了甲、乙两个图(如图所示)呢~~~
请你根据王晓的描述和王晓爸爸所画的图,回答下列问题.
(1)经测量甲图中∠BAC=30°,∠BCD=30°,试判断△CBD与△FAD是否相似,并说明理由;
(2)在乙图中∠BAC≠30°,请你求证:
+
=2.
爸爸说:当然!我根据你的描述画了甲、乙两个图(如图所示)呢~~~
请你根据王晓的描述和王晓爸爸所画的图,回答下列问题.
(1)经测量甲图中∠BAC=30°,∠BCD=30°,试判断△CBD与△FAD是否相似,并说明理由;
(2)在乙图中∠BAC≠30°,请你求证:
| AB |
| AD |
| AE |
| AF |

考点:相似三角形的判定与性质
专题:
分析:(1)如图甲,证明∠B=∠DAF,∠BDC=∠ADF,即可解决问题.
(2)如图乙,作辅助线;证明
=
;证明BD=DM(设为λ),设AM=μ;得到AD=λ+μ,AB=2λ+μ,即可解决问题.
(2)如图乙,作辅助线;证明
| AE |
| AF |
| AM |
| AD |
解答: 解:(1)△CBD∽△FAD;理由如下:
解:(1)△CBD∽△FAD;理由如下:
如图甲,∵∠BAC=30°,
∠BCD=30°,∠B=60°,
∴∠BDC=∠BCA=90°;
AC⊥BE,而BC=CE,
∴AB=AE,∠BAC=∠EAC=30°,
∴∠DAF=60°,
∴∠B=∠DAF,∠BDC=∠ADF,
∴△CBD∽△FAD.
(2)如图乙,过点作EM∥DF;
则△AME∽△ADF,
∴
=
;
∵BC=CE,CD∥ME,
∴BD=DM(设为λ),设AM=μ;
∴AD=λ+μ,AB=2λ+μ;
∴
+
=
+
=
=2,
即
+
=2.
 解:(1)△CBD∽△FAD;理由如下:
解:(1)△CBD∽△FAD;理由如下:如图甲,∵∠BAC=30°,
∠BCD=30°,∠B=60°,
∴∠BDC=∠BCA=90°;
AC⊥BE,而BC=CE,
∴AB=AE,∠BAC=∠EAC=30°,
∴∠DAF=60°,
∴∠B=∠DAF,∠BDC=∠ADF,
∴△CBD∽△FAD.
(2)如图乙,过点作EM∥DF;
则△AME∽△ADF,
∴
| AE |
| AF |
| AM |
| AD |
∵BC=CE,CD∥ME,
∴BD=DM(设为λ),设AM=μ;
∴AD=λ+μ,AB=2λ+μ;
∴
| AB |
| AD |
| AE |
| AF |
| 2λ+μ |
| λ+μ |
| μ |
| λ+μ |
=
| 2(λ+μ) |
| λ+μ |
即
| AB |
| AD |
| AE |
| AF |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造相似三角形;运用相似三角形的性质来分析、判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列调查中,适宜采用全面调查(普查)的是( )
| A、对全国中学生心理健康现状的调查 |
| B、对冷饮市场上冰淇淋质量情况的调查 |
| C、对西安市市民实施低碳生活情况的调查 |
| D、对“神舟九号”飞船零部件状况的检查 |
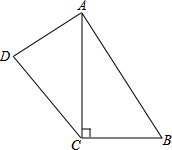 已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9.
已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9. 如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6).
如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6). 如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.
如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.