题目内容
19.问题情境:小明在学习中发现:棱长为1cm的正方体的表面展开图面积为6cm2.但是反过来,在面积为6cm2的长方形纸片(如图1,图中小正方形的边长为1cm)上是画不出这个正方体表面展开图的.于是,爱思考的小明就想:要画出这个正方体的表面展开图,最少需要选用多大面积的长方形纸片呢?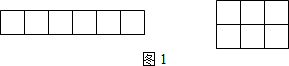
问题解决:小明仔细研究正方体的表面展开图的11种不同情形后发现,至少要用用“2×5”和“3×4”两种不同的长方形纸片才能剪得一个正方体的表面展开图.
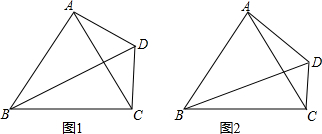
(1)请你在下面两个网格中分别画出一种;
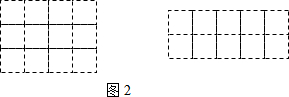
(2)比较发现:用长方形纸片剪得一个正方体的表面展开图的最大利用率为60%.
拓展延伸:若要在如图3所示的“2×8”和“3×6”的两种规格的长方形纸片上分别剪出两个正方体的表面展开图,请在图中画出裁剪方法.
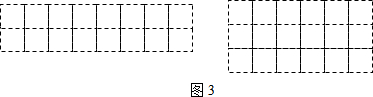
操作应用:
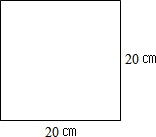
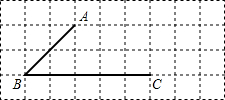
现有边长20cm的正方形纸片(图4所示),能否用它剪得两个面积最大的正方体表面展开图?若能,请你画出你的设计方案;若不能,请说明理由.
分析 根据正方体展开图的11种特征,正方体展开图分四种类型.“1-4-1”结构,“2-2-2”结构,“1-3-2”结构,“3-3”结构,发现至少要用“2×5”和“3×4”两种不同的长方形纸片才能剪得一个正方体的表面展开图,进行分析.
解答 解:根据正方体展开图的11种特征,正方体展开图分四种类型.
∵“1-4-1”结构,“2-2-2”结构,“1-3-2”结构所需的长方形长是4个边长1厘米的正方形的边长,宽是3个边长1厘米的正方形的边长,
∴此长方形的面积为12cm2;
∵“3-3”结构,所需长方形的长是5个边长1厘米的正方形的边长,宽是2个边长1厘米的正方形的边长,
∴长方形的面积为10cm2,
∴要画出这个正方体的表面展开图,最少需要选用10cm2的长方形纸片.
(1)如图2:
(2)∵正方体的表面展开图,最少需要选用10cm2的长方形纸片,正方体的表面积为6cm2,
∴用长方形纸片剪得一个正方体的表面展开图的最大利用率为:$\frac{6}{10}×100%$=60%,
故答案为:60%.
(3)如图3:
(4)能,如图4,
点评 本题考查了作图,解决本题的关键是掌握正方体展开图的11种特征.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
12.无理数a满足:2<a<3,那么a可能是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | 2.5 | D. | $\frac{20}{7}$ |
14.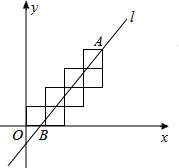 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{9}$ |
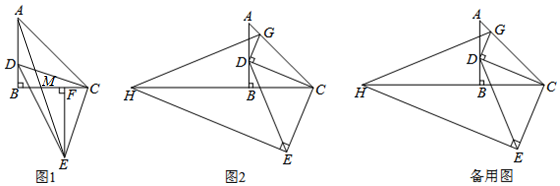
9.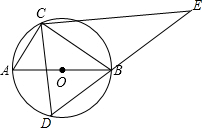 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题: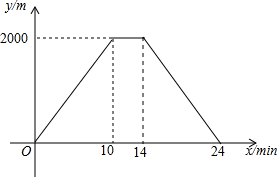 小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系.
小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系.