题目内容
7.(1)解方程:$\frac{3}{x-1}-1=\frac{1}{1-x}$(2)解不等式组:$\left\{\begin{array}{l}-2x<5\\ 2x+3≤-7(x+1)\end{array}\right.$.
分析 (1)分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:3-(x-1)=-1,
去括号得:3-x+1=-1,
解得:x=5,
经经验x=5是原方程的解;
(2)$\left\{\begin{array}{l}{-2x<5①}\\{2x+3≤-7(x+1)②}\end{array}\right.$
解不等式①得:x>-$\frac{5}{2}$;
解不等式②得:x≤-$\frac{10}{9}$,
则原不等式组的解集是-$\frac{5}{2}$<x≤-$\frac{10}{9}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 8x+4=12x | B. | 4y-4=y | C. | 4y-3y=y | D. | 3x-x=3 |
15.在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
12.无理数a满足:2<a<3,那么a可能是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | 2.5 | D. | $\frac{20}{7}$ |
16.在0,-2,-1,3这四个数中,最小的数是( )
| A. | 3 | B. | -1 | C. | 0 | D. | -2 |
14.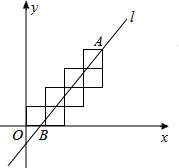 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{9}$ |
 如图,A点坐标为(-2,0),B点坐标为(0,-3).
如图,A点坐标为(-2,0),B点坐标为(0,-3).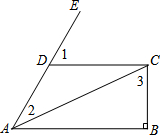 如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°.
如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°.