题目内容
2.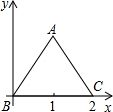 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
分析 根据等边三角形的性质求出点A的坐标,根据题意和旋转的性质可知点A的对应点与点A关于y轴对称,求出点A的对应点的坐标.
解答 解:∵△ABC是等边三角形,AB=2,
∴点A的坐标为(1,$\sqrt{3}$),
∵∠ABC=60°,
∴AB与y轴的夹角为30°,
等边△ABC以点B为旋转中心,逆时针旋转60°时,
点A的对应点与点A关于y轴对称,
∴点A的对应点的坐标为(-1,$\sqrt{3}$),
故选:C.
点评 本题考查的是等边三角形的性质和旋转变换的知识,根据题意求出点A的坐标和确定点A的对应点与点A关于y轴对称是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
16.在0,-2,-1,3这四个数中,最小的数是( )
| A. | 3 | B. | -1 | C. | 0 | D. | -2 |
14.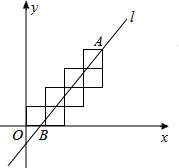 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{9}$ |
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题: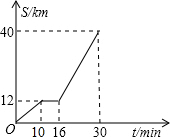 如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题: