题目内容
10.化简:(1)$\frac{4}{{x}^{2}-4}$+$\frac{2}{x+2}$-$\frac{1}{x-2}$;
(2)$\frac{x-4}{4{x}^{2}-9}$÷$\frac{1}{2x+3}$+$\frac{x+1}{2x-3}$;
(3)1-$\frac{a-1}{a}$÷($\frac{a}{a+2}$-$\frac{1}{{a}^{2}+2a}$).
分析 结合分式混合运算的运算法则进行求解即可.
解答 解:(1)原式=$\frac{4}{(x+2)(x-2)}$+$\frac{2(x-2)}{(x+2)(x-2)}$-$\frac{x+2}{(x-2)(x+2)}$
=$\frac{x-2}{(x+2)(x-2)}$
=$\frac{1}{x+2}$.
(2)原式=$\frac{x-4}{(2x+3)(2x-3)}$×(2x+3)+$\frac{x+1}{2x-3}$
=$\frac{x-4}{2x-3}$+$\frac{x+1}{2x-3}$
=$\frac{2x-3}{2x-3}$
=1.
(3)原式=1-$\frac{a-1}{a}$÷($\frac{{a}^{2}}{{a}^{2}+2a}$-$\frac{1}{{a}^{2}+2a}$)
=1-$\frac{a-1}{a}$÷$\frac{(a-1)(a+1)}{{a}^{2}+2a}$
=1-$\frac{a-1}{a}$×$\frac{a(a+2)}{(a-1)(a+1)}$
=1-$\frac{a+2}{a+1}$
=-$\frac{1}{a+1}$.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的运算法则.

练习册系列答案
相关题目
1.已知⊙O1与⊙O2的半径分别是2和6,若⊙O1与⊙O2相交,那么圆心距O1O2的取值范围是( )
| A. | 2<O1O2<4 | B. | 2<O1O2<6 | C. | 4<O1O2<8 | D. | 4<O1O2<10 |
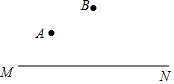 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理. 如图,长方形ABCD的面积为$\sqrt{18}$cm2,AB=$\sqrt{3}$cm,求边BC的长.
如图,长方形ABCD的面积为$\sqrt{18}$cm2,AB=$\sqrt{3}$cm,求边BC的长.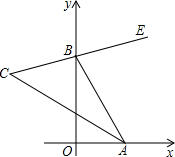 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.