题目内容
10.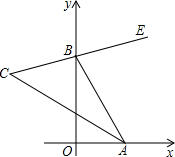 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
分析 由BE平分∠ABF、CA平分∠OAB知2∠EBA=∠ABF、∠OAB=2∠CAB,根据△AOB外角性质得∠ABF=∠AOB+∠OAB,即∠ABF=90°+∠OAB,再根据△ACB外角性质得∠EBA=∠C+∠CAB,即90°+∠OAB=2(∠C+∠CAB),从而知90°+∠OAB=2∠C+∠OAB,即可得∠C=45°.
解答 解:∠ACB的大小不发生改变,
如图,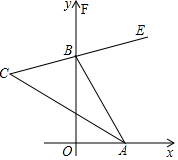
∵BE平分∠ABF,CA平分∠OAB,
∴2∠EBA=∠ABF,∠OAB=2∠CAB,
又∵∠ABF为△AOB的外角,
∴∠ABF=∠AOB+∠OAB,
∵∠AOB=90°,
∴∠ABF=90°+∠OAB,
又∵∠EBA为△ACB的外角,
∴∠EBA=∠C+∠CAB,
∴90°+∠OAB=2(∠C+∠CAB),
90°+∠OAB=2∠C+∠OAB,
∴∠C=45°,
即∠ACB的大小不发生改变.
点评 本题主要考查角平分线性质、三角形外角的性质等知识点,由∠ACB联想到△ACB外角∠EBA,继而由角平分线的性质联想到△AOB外角是解题的关键.

练习册系列答案
相关题目
1.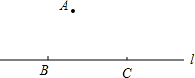 如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )
如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )
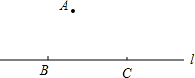 如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )
如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )| A. | 平行四边形 | B. | 梯形 | ||
| C. | 平行四边形或梯形 | D. | 平行四边形或矩形 |
18.⊙O的半径为6,弦长为一元二次方程x2-5x-6=0的两根,则弦到圆心的距离及弦所对的圆心角的度数分别是( )
| A. | $\sqrt{3}$和30° | B. | $\sqrt{3}$和60° | C. | 3$\sqrt{3}$和30° | D. | 3$\sqrt{3}$和60° |
15.如果两条直线被第三条直线所截,那么一对内错角的平分线的位置关系是( )
| A. | 互相垂直 | B. | 互相平行 | C. | 相交但不垂直 | D. | 不能确定 |
2.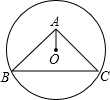 在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
 在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )
在等腰直角△ABC中,∠BAC=90°,BC=6,⊙O的圆心O在△ABC内部,且经过B、C两点,若OA=1,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
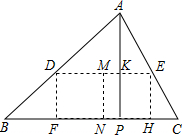 如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.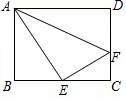 如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$.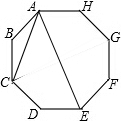 如图,在正八边形ABCDEFGH中,AC、AE是对角线,则sin∠CAE的值为$\frac{\sqrt{2}}{2}$.
如图,在正八边形ABCDEFGH中,AC、AE是对角线,则sin∠CAE的值为$\frac{\sqrt{2}}{2}$.