题目内容
18.已知y=(a+3)x${\;}^{{a}^{2}+a-10}$是关于x的二次函数(1)求a的值;
(2)a为何值时,抛物线有最低点?这时当x为何值时,y随x的增大而增大?
(3)a为何值时,函数有最大值?这时当x为何值时,y随x的增大而减小?
分析 (1)根据二次函数的定义求出a的值即可解决问题.
(2)运用当二次项系数大于0时,抛物线开口向上,图象有最低点;在对称轴的右侧y随x的增大而增大.
(3)运用当二次项系数小于0时,抛物线开口向下,图象有最高点;在对称轴的右侧y随x的增大而减小.
解答 解:(1)∵函数y=(a+3)x${\;}^{{a}^{2}+a-10}$是关于x的二次函数,
∴a2+a-10=2,a+3≠0,
解得:a=3或a=-4.
(2)∵a=3,
∴a+3=6>0,
当a=3时,抛物线有最低点;
当x>0时,y随x的增大而增大.
(3)当a=-4时,
a+3=-1<0,
函数有最大值,最大值是0;
当x>0时,y随x的增大而减小.
点评 该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.

练习册系列答案
相关题目
18.⊙O的半径为6,弦长为一元二次方程x2-5x-6=0的两根,则弦到圆心的距离及弦所对的圆心角的度数分别是( )
| A. | $\sqrt{3}$和30° | B. | $\sqrt{3}$和60° | C. | 3$\sqrt{3}$和30° | D. | 3$\sqrt{3}$和60° |
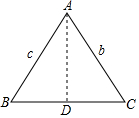 利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)
利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC) (尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法)
(尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法)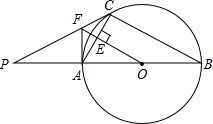 如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P. 如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.
如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.