题目内容
2.将抛物线y=2(x-1)2-1沿着对称轴平移,当抛物线经过点P(2,3)时,求此时的抛物线解析式,并指出平移的方向和平移的单位.分析 根据抛物线的性质得抛物线y=2(x-1)2-1的对称轴为直线x=1,顶点坐标为(1,-1),则可设平移后的顶点坐标为(1,-1+t),于是得到平移后的抛物线解析式为y=2(x-1)2-1+t,再把P点坐标代入求出t,从而可确定平移后的抛物线解析式,也可得到平移的方向和平移的单位.
解答 解:抛物线y=2(x-1)2-1的对称轴为直线x=1,顶点坐标为(1,-1),
设平移后的顶点坐标为(1,-1+t),则平移后的抛物线解析式为y=2(x-1)2-1+t,
把P(2,3)代入得2(2-1)2-1+t=3,解得t=2,
所以平移后的抛物线解析式为y=2(x-1)2+1,
把抛物线y=2(x-1)2-1沿直线x=1向上平移2个单位得到y=2(x-1)2+1.
点评 本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
7.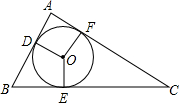 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )| A. | 90°,60°,30° | B. | 80°,60°,40° | C. | 90°,50°,40° | D. | 80°,70°,30° |
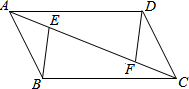 如图,在四边形ABCD中,点E、F在AC上,有下面五个论断:
如图,在四边形ABCD中,点E、F在AC上,有下面五个论断: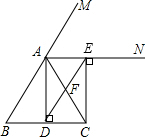 如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F.
如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F. 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°
如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°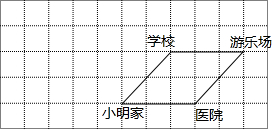 位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示.
位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示.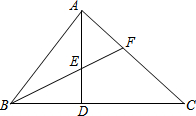 在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.
在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.