题目内容
12.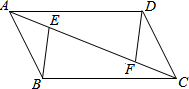 如图,在四边形ABCD中,点E、F在AC上,有下面五个论断:
如图,在四边形ABCD中,点E、F在AC上,有下面五个论断:①AD=CB;②AB=CD;③AE=CF;④∠EBC=∠ADF;⑤AD∥BC.
将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.用序号写出一个真命题(书写形式如:如果×××,那么××),并给出证明.
分析 由AD∥BC,AE=CF,∠EBC=∠ADF,利用AAS易证△BEC≌△DFA,进而有BC=AD.
解答 解:如果AD∥BC,AE=CF,∠EBC=∠ADF,那么BC=AD,
∵AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AC-AE=AC-CF,
即AF=CE,
在△BEC与△DFA中
$\left\{\begin{array}{l}{∠EBC=∠ADF}\\{∠DAF=∠DCE}\\{AF=CE}\end{array}\right.$,
∴△BEC≌△DFA(AAS),
∴AD=BC
点评 此题考查全等三角形的判定和性质,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
2.若等腰三角形腰上的高是底边的一半,则这个等腰三角形的底角是( )
| A. | 75°或30° | B. | 30° | C. | 15° | D. | 75°和15° |
7.有一组按规律排列的数:1,2,4,8,16,32,…,第2012个数应是( )
| A. | 22012 | B. | 22011 | C. | 22010 | D. | 22009 |
 五一黄金周,公司组织员工到A,B,C三地旅游,公司购买前往各地的车票种类,数量绘制成条形统计图,如图.根据图表回答:
五一黄金周,公司组织员工到A,B,C三地旅游,公司购买前往各地的车票种类,数量绘制成条形统计图,如图.根据图表回答: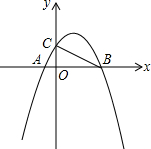 如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.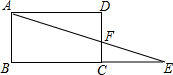 如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.
如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.