题目内容
7.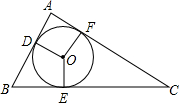 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )| A. | 90°,60°,30° | B. | 80°,60°,40° | C. | 90°,50°,40° | D. | 80°,70°,30° |
分析 利用切线的性质得出∠ODB=∠OEB=∠OEC=∠OFC=90°,进而利用四边形内角和定理以及三角形内角和定理得出答案.
解答 解:∵⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,
∴∠ODB=∠OEB=∠OEC=∠OFC=90°,
又∵∠DOE=120°,∠EOF=150°,
∴∠B=360°-120°-90°-90°=60°,
∠C=360°-150°-90°-90°=30°,
∴∠A=180°-∠B-∠C=90°.
故选:A.
点评 此题主要考查了切线的性质以及四边形内角和定理以及三角形内角和定理,熟练应用切线的性质定理是解题关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
18.如图,函数y=-x(x<0)的图象是( )
| A. |  | B. |  | C. |  | D. |  |
11.某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
根据规定,笔试成绩和面试成绩分别占总成绩的40%和60%.
(1)这5名选手笔试成绩的中位数是84分,众数是84分.
(2)现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分,求出其余两名选手的综合成绩,并确定谁将被录取?
| 序号项目 | 1 | 2 | 3 | 4 | 5 |
| 笔试成绩/分 | 85 | 84 | 84 | 90 | 80 |
| 面试成绩/分 | 90 | 86 | 80 | 90 | 85 |
(1)这5名选手笔试成绩的中位数是84分,众数是84分.
(2)现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分,求出其余两名选手的综合成绩,并确定谁将被录取?
8.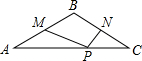 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )| A. | 2+$\sqrt{3}$ | B. | 4 | C. | 4+2$\sqrt{3}$ | D. | 12 |
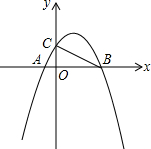 如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.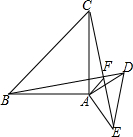 如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.