题目内容
3.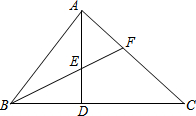 在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.
在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.(1)求证:AD⊥BC(请用一对互逆命题进行证明)
(2)写出你所用到的这对互逆命题.
分析 (1)根据直角三角形的两锐角互余和角平分线的定义解答即可;
(2)根据直角三角形的性质写出互逆命题即可.
解答  (1)证明:在直角△ABC中,
(1)证明:在直角△ABC中,
∵∠BAC=90°
∴∠1+∠AFE=90°
∵BF平分∠ABC
∴∠1=∠2
∵∠AEF=∠AFE
又∵∠3=∠AEF
∴∠3=∠AFE
∴∠2+∠3=90°
∴∠BDE=90°
∴AD⊥BC;
(2)互逆命题:直角三角形的两锐角互余;有两个锐角互余的三角形是直角三角形.
点评 本题考查的是直角三角形的性质和判定以及命题与定理,掌握角平分线的定义和三角形内角和定理是解题的关键,注意互逆命题题设和结论的关系.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
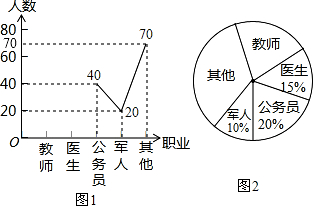
11.某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
根据规定,笔试成绩和面试成绩分别占总成绩的40%和60%.
(1)这5名选手笔试成绩的中位数是84分,众数是84分.
(2)现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分,求出其余两名选手的综合成绩,并确定谁将被录取?
| 序号项目 | 1 | 2 | 3 | 4 | 5 |
| 笔试成绩/分 | 85 | 84 | 84 | 90 | 80 |
| 面试成绩/分 | 90 | 86 | 80 | 90 | 85 |
(1)这5名选手笔试成绩的中位数是84分,众数是84分.
(2)现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分,求出其余两名选手的综合成绩,并确定谁将被录取?
8.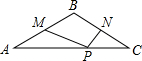 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )| A. | 2+$\sqrt{3}$ | B. | 4 | C. | 4+2$\sqrt{3}$ | D. | 12 |
13.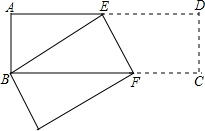 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
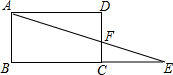 如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.
如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$. 如图,已知EF∥AD,∠1=∠2,∠BAC=78°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=78°,求∠AGD的度数.