题目内容
12. 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
分析 (1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例函数的解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解;
(3)根据函数的图象和交点坐标即可求解.
解答 解:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=$\frac{OA}{OB}$=$\frac{CE}{BE}$=$\frac{1}{2}$,
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,
∴$\left\{\begin{array}{l}{4a+b=0}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$.
故直线AB的解析式为y=-$\frac{1}{2}$x+2.
∵反比例函数y=$\frac{k}{x}$的图象过C,
∴3=$\frac{k}{-2}$,
∴k=-6.
∴该反比例函数的解析式为y=-$\frac{6}{x}$; (2)联立反比例函数的解析式和直线AB的解析式可得$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{6}{x}}\end{array}\right.$,
(2)联立反比例函数的解析式和直线AB的解析式可得$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{6}{x}}\end{array}\right.$,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8;
(3)由图象得,一次函数的值大于反比例函数的值时x的取值范围:x<-2或0<x<6.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案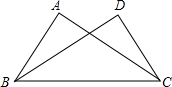 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是AB=DC.
如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是AB=DC.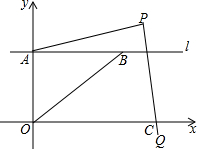 如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,
如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,