题目内容
14．（1）化简：$\frac{x}{x+1}$+$\frac{3x+1}{{x}^{2}-1}$（2）解不等式组：$\left\{\begin{array}{l}{x-2≥3x}\\{\frac{x}{2}+2＜-3}\end{array}\right.$．
分析 （1）根据分式的运算法则即可求出答案．
（2）根据不等式组的解法即可求出答案
解答 解：（1）原式=$\frac{x（x-1）}{{x}^{2}-1}$+$\frac{3x+1}{{x}^{2}-1}$
=$\frac{{x}^{2}-x+3x+1}{{x}^{2}-1}$
=$\frac{（x-1）^{2}}{{x}^{2}-1}$
=$\frac{x-1}{x+1}$
（2）由x-2≥3x，
∴x≤-1
由$\frac{x}{2}$+2＜-3
∴x＜-10
∴不等式组的解集为：x＜-10
点评 本题考查学生的计算能力，解题的关键是熟练运用分式运算法则以及一元一次不等式组的解法，本题属于基础题型．
练习册系列答案
相关题目
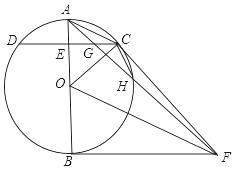如图，已知AB是⊙O的直径，C是⊙O上任一点（不与A，B重合），AB⊥CD于E，BF为⊙O的切线，OF∥AC，连结AF，FC，AF与CD交于点G，与⊙O交于点H，连结CH．
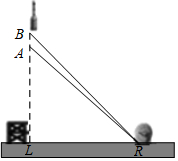2016年2月1日，我国在西昌卫星发射中心，用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道，如图，火箭从地面L处发射，当火箭达到A点时，从位于地面R处雷达站测得AP的距离是6km．仰角为42.4°；1秒后火箭到达B点，此时测得仰角为45.5°．（参考数据：sin42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70，tan45.5°≈1.02）．
如图，点P是线段AB外一点，请用尺规求作点Q，使得四边形QPAB是平行四边形．（保留作图痕迹，不写作法）．