题目内容
7．当x满足-3＜x＜5时，$\frac{5-3x}{2}$的值大于-5而小于7．分析 根据题意列出不等式组，分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：根据题意，得：$\left\{\begin{array}{l}{\frac{5-3x}{2}＞-5}&{①}\\{\frac{5-3x}{2}＜7}&{②}\end{array}\right.$，
解不等式①，得：x＜5，
解不等式②，得：x＞-3，
则不等式组的解集为-3＜x＜5，
故答案为：-3＜x＜5．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
10．下列计算正确的是（ ）
| A． | （-3a2b）3=-3a5b3 | B． | $\frac{1}{2}$ab2•（-4a3b）=-2a4b3 | ||
| C． | 4m3n2÷m3n2=0 | D． | a5-a2=a3 |
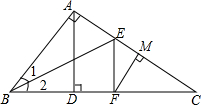如图，△ABC中，∠BAC=90°，AD⊥BC，BE平分∠ABC，EF⊥BC，FM⊥AC，垂足分别是D，F，M，求证：FM=FD．
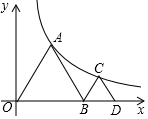如图，△ADB、△BCD均为等边三角形，顶点A、C均在反比例函数y=$\frac{k}{x}$（x＞0）图象上，若点A的坐标是（1，a），则点C的横坐标为1+$\sqrt{2}$．