题目内容
3.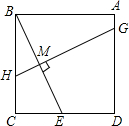 如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )| A. | 4:1 | B. | 3:1 | C. | 3:2 | D. | 5:2 |
分析 根据正方形的性质结合全等三角形的判定方法得出△BCE≌△HFG(ASA),则BE=HG,再推出△BHM∽△BEC,进而利用相似三角形的性质得出答案.
解答 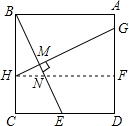 解:过点H作HF⊥AD于点F,交BE于点N,
解:过点H作HF⊥AD于点F,交BE于点N,
由题意可得:∠BHM+∠GHF=90°,
∠HBM+∠BHM=90°,
则∠CBE=∠GHF,
在△BCE和△HFG中,
$\left\{\begin{array}{l}{∠CBE=∠FHG}\\{BC=HF}\\{∠C=∠HFG}\end{array}\right.$,
∴△BCE≌△HFG(ASA),
∴BE=HG,
∵∠BMH=∠C,∠CBE=∠MBH,
∴△BHM∽△BEC,
∵E为CD的中点,
∴$\frac{CE}{BC}$=$\frac{HM}{BM}$=$\frac{1}{2}$,
设HM=x,则BM=2x,故BE=HG=4x,
则MG=4x-x=3x,
故GM:MH的值为:3:1.
故选:B.
点评 此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质、正方形的性质等知识,正确得出BE=HG是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.下列四个命题中,其中真命题是( )
| A. | 两条直线被第三条直线所截,同旁内角互补 | |
| B. | 两个锐角之和一定是钝角 | |
| C. | 三角形的任何一个内角大于一个外角 | |
| D. | 内错角相等,两直线平行 |
16.某商场购进一批服装,每件进价为100元,由于换季滞销,商场决定将这种服装按标价的7折销售,若打折后每件服装仍能获利5%,则该服装的标价是( )
| A. | 150元 | B. | 140元 | C. | 130元 | D. | 120元 |
13.直线y=-3x-2与直线y=2x+8的交点坐标是( )
| A. | (-2,4) | B. | (-2,-4) | C. | (2,4) | D. | (2,-4) |
 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.

 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标.(1)以点(3,6)为位似中心,在网格中将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1.请在网格内画出△A1B1C1,并写出点A1的坐标:(-1,4);
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标.(1)以点(3,6)为位似中心,在网格中将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1.请在网格内画出△A1B1C1,并写出点A1的坐标:(-1,4);