题目内容

13．直线y=-3x-2与直线y=2x+8的交点坐标是（　　）
A．（-2，4）B．（-2，-4）C．（2，4）D．（2，-4）

分析 求两条直线的交点，可联立两函数的解析式，所得方程组的解即为两个函数的交点坐标．

解答 解：联立两函数的解析式组成方程组得：
$\left\{\begin{array}{l}{y=-3x-2}\\{y=2x+8}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$，
则直线y=-3x-2与直线y=2x+8的交点坐标是（-2，4）．
故选：A．

点评 本题考查了两条直线相交问题，关键理解两条直线相交的交点即是两个函数联立方程组求得的解．

练习册系列答案
相关题目
3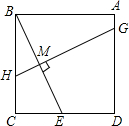．如图所示，在正方形ABCD中，E为CD的中点，作BE的中垂线GH，垂足为M，则GM：MH的值为（　　）
A．4：1B．3：1C．3：2D．5：2
4．下列事件中，最适合使用普查方式收集数据的是（　　）
A．了解扬州人民对建设高铁的意见B．了解本班同学的课外阅读情况
C．了解同批次LED灯泡的使用寿命D．了解扬州市八年级学生的视力情况
1．解方程$\frac{x-1}{4}=3-\frac{1+2x}{8}$去分母正确的是（　　）
A．2（x-1）=24-1-2xB．2（x-1）=24-1+2xC．2（x-1）=3-1-2xD．2（x-1）=3-1+2x
8．如图，在梯形ABCD中，AD∥BC，点E、F分别是AB、CD的中点，我们把线段EF称为梯形ABCD的中位线，通过观察、测量，猜想EF和AD，BC有怎样的位置关系和数量关系，并证明你的结论．
18．把不等式组$\left\{\begin{array}{l}{2x＞-4}\\{x-2≤0}\end{array}\right.$的解集表示在数轴上，正确的是（　　）
A．B．C．D．
5．解下列分式方程．
（1）$\frac{1}{x-2}$=$\frac{1}{3x}$
（2）$\frac{2}{2x-1}+\frac{1}{2x-1}$=1
（3）$\frac{1}{x+1}+\frac{1}{x-1}=\frac{2}{{{x^2}-1}}$．
2．解不等式组，并把它的解集在数轴上表示出来：
（1）$\left\{\begin{array}{l}{2x+1＞0}\\{x＞2x-5}\end{array}\right.$                 
（2）$\left\{\begin{array}{l}{3（x+2）＞x+8}\\{\frac{x}{4}＞\frac{x-1}{3}}\end{array}\right.$．
3．若a和b都是有理数，则下列①若a≠b，则a2≠b2；②若a＞b，则a2＞b2；③若a＞b，则|a|＞|b|；④若a2＞b2，则a＞b说法中，正确的个数是（　　）
A．0个B．1个C．2个D．3个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网