题目内容
11. 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.(1)求证:BE=CF;
(2)设AD、EF相交于G,若EF=8,⊙O的半径为5,求DG的长.
分析 (1)连接DE,DF,由AB=AC,且AD为BC边上的高,利用三线合一得到D为BC的中点,AD为顶角平分线,再由AD为圆O的直径,利用直角所对的角为直角得到一对直角相等,利用AAS得到三角形EBD与三角形FCD全等,由全等三角形的对应边相等得到BE=CF,得证;
(2)由(1)AB=AC,BE=CF知AE=AF,又∠BAD=∠CAD根据等腰三角形三线合一知AD垂直平分EF;连接OE,设DG=x,分别表示出OE、OG、EF的长,根据勾股定理可得x的值.
解答 解:(1)证明:如图,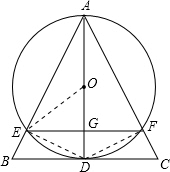
连接DE、DF、OE,
∵AB=AC,AD⊥BC,
∴∠B=∠C,BD=CD,∠BAD=∠CAD
∵AD为⊙O的直径,
∴∠DEA=∠DFA=90°,
在△DBE和△DCF中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠B=∠C}\\{BD=CD}\end{array}\right.$,
∴△DBE≌△DCF(AAS),
∴BE=CF;
(2)∵AB=AC,BE=CF,
∴AE=AF,
∵∠BAD=∠CAD,EF=8
∴AD⊥EF,EG=FG=$\frac{1}{2}$EF=4,
设DG=x,
∵⊙O的半径为5,
∴OE=5,OG=5-x,
在RT△OEG中,∵OE2=EG2+OG2,
∴52=42+(5-x)2,
解得:x1=2,x2=8(舍去).
故DG的长为2.
点评 此题考查了全等三角形的判定与性质,勾股定理,以及等腰三角形的性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
3.老师让同学们举一个y是x的函数的例子,同学们分别用表格、图象、函数表达式列举了如下4个x、y之间的关系:
其中y一定是x的函数的是④.(填写所有正确的序号)
①
| ② | ||||||||||
| ③ y=kx+b | ④ y=|x| |
4.顺次连接四边形ABCD各边的中点,所得四边形是( )
| A. | 平行四边形 | B. | 对角线互相垂直的四边形 | ||
| C. | 矩形 | D. | 菱形 |
3.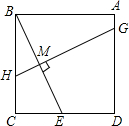 如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
 如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )| A. | 4:1 | B. | 3:1 | C. | 3:2 | D. | 5:2 |
1.解方程$\frac{x-1}{4}=3-\frac{1+2x}{8}$去分母正确的是( )
| A. | 2(x-1)=24-1-2x | B. | 2(x-1)=24-1+2x | C. | 2(x-1)=3-1-2x | D. | 2(x-1)=3-1+2x |
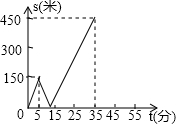 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示. 已知:抛物线y=-x2-2x+3与x轴相交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为P.
已知:抛物线y=-x2-2x+3与x轴相交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为P.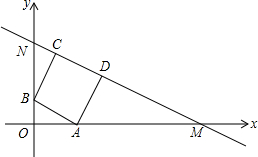 在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).
在直角坐标系中,直线MN分别交x轴、y轴的正半轴于点N、M,正方形ABCD内接于Rt△MON,点A、B分别在线段MO、NO上,点C、D在线段MN上.若点D的坐标为(7,4),则点C坐标(3,7).