题目内容
15.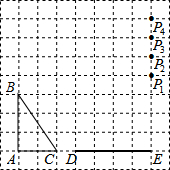 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3.
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3.
分析 由于∠BAC=∠PED=90°,而$\frac{AB}{AC}$=$\frac{3}{2}$,则当$\frac{EP}{ED}$=$\frac{3}{2}$时,可根据两组对应边的比相等且夹角对应相等的两个三角形相似判断△ABC∽△EPD,然后利用DE=4,所以EP=6,则易得点P落在P3处.
解答 解:∵∠BAC=∠PED,
而$\frac{AB}{AC}$=$\frac{3}{2}$,
∴$\frac{EP}{ED}$=$\frac{3}{2}$时,△ABC∽△EPD,
∵DE=4,
∴EP=6,
∴点P落在P3处.
故答案为:P3.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
相关题目
20.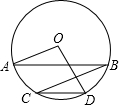 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )
如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=20°,CD=OD,则∠AOD的度数是( )| A. | 120° | B. | 140° | C. | 110° | D. | 100° |
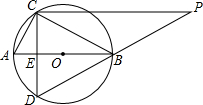 如图,AB为⊙O直径,C为圆上一点,AC=2,BC=4,E为直径AB上一动点(不与点A、B重合),CE延长线交⊙O于D,PC⊥CD交DB延长线于点P.
如图,AB为⊙O直径,C为圆上一点,AC=2,BC=4,E为直径AB上一动点(不与点A、B重合),CE延长线交⊙O于D,PC⊥CD交DB延长线于点P.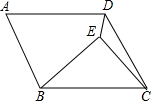 如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?
如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?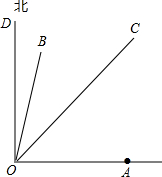 如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.
如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.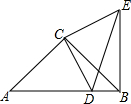 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$.点D在边AB上,不与点A,B重合,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$.点D在边AB上,不与点A,B重合,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE.