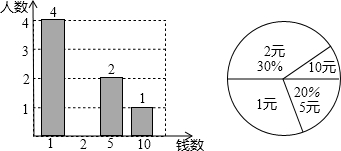
题目内容
4.解下列分式方程:(1)$\frac{x}{2x-3}$+$\frac{5}{3-2x}$=4;
(2)$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$
(3)$\frac{x}{x+1}$-1=$\frac{3}{{x}^{2}-x-2}$.
分析 各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x-5=8x-12,
解得:x=1,
经检验x=1是分式方程的解;
(2)去分母得:2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:x(x-2)-x2+x+2=3,
解得:x=-1,
经检验x=-1是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
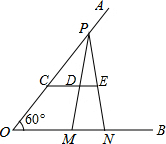 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,点C为线段OP上任意一点,CD∥ON交PM、PN分别为D、E.若MN=3,则$\frac{CD}{DE}$的值为$\frac{7}{6}$.
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,点C为线段OP上任意一点,CD∥ON交PM、PN分别为D、E.若MN=3,则$\frac{CD}{DE}$的值为$\frac{7}{6}$.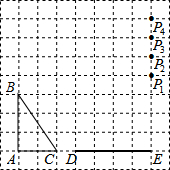 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3.
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3. 已知:如图,∠AOD=∠BOC,∠A=∠C,O是AC的中点.
已知:如图,∠AOD=∠BOC,∠A=∠C,O是AC的中点.