题目内容
20．
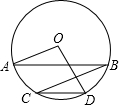如图，在⊙O中，弦AB∥CD，连接BC，OA，OD．若∠BCD=20°，CD=OD，则∠AOD的度数是（ ）| A． | 120° | B． | 140° | C． | 110° | D． | 100° |
分析 连结OC，如图，先利用平行线的性质得∠ABC=∠BCD=20°，再根据圆周角定理得到AOC=2∠ABC=40°，接着判断△OCD为等边三角形，得到∠COD=60°，则易得∠AOD=100°．
解答 解：连结OC，如图，
∵AB∥CD，
∴∠ABC=∠BCD=20°，
∴∠AOC=2∠ABC=40°，
∵CD=OD，
而OC=OD，
∴△OCD为等边三角形，
∴∠COD=60°，
∴∠AOD=40°+60°=100°．
故选D．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
8．
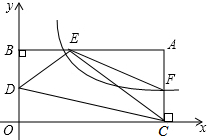如图，点A在直角坐标系xOy第一象限中，AB⊥y轴于点B，AC⊥x轴于点C，点D是BO的中点，反比例函数y=$\frac{k}{x}$的图象交AB于点E，交AC于点F，且满足AE=2BE．若△DEC的面积为1，则△AEF的面积为（ ）
如图，点A在直角坐标系xOy第一象限中，AB⊥y轴于点B，AC⊥x轴于点C，点D是BO的中点，反比例函数y=$\frac{k}{x}$的图象交AB于点E，交AC于点F，且满足AE=2BE．若△DEC的面积为1，则△AEF的面积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | 1 |
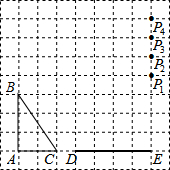如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为P3．
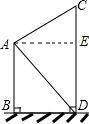如图，甲楼的底端B处与乙楼的底端D处相距50m，从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°．从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35．分别求甲楼AB和乙楼CD的高为多少m（精确到1m）．（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
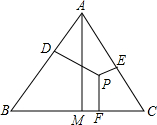已知，如图所示：P为等边三角形ABC内的一点，它到三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高AM=h．则h与 h1、h2、h3有何数量关系？写出你的猜想并加以证明．