题目内容
1. 如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.
如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.(1)求证:∠AEF=∠BCE;
(2)当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;
(3)探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.
分析 (1)根据三角形的外角的性质即可得到结论;
(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA,根据垂径定理得到BM=AM=$\frac{AB}{2}$=3,根据勾股定理得到CF=CM=4,根据相似三角形的性质得到$\frac{EA}{BC}=\frac{AF}{BE}$,设BE长为x,则EA长为6-x即可得到结论;
(3)①当CE=CF时推出EF∥AB,此时E与B重合,与条件矛盾,不成立.②当CF=EF时,根据全等三角形的性质得到BE=AB-5=1,③当CF=EF时,根据相似三角形的性质即可得到结论.
解答  (1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
(1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
∵∠CEF=∠B,
∴∠AEF=∠BCE;
(2)解:如图1,设⊙C与BA切于点M,则CM=CF,CM⊥BA,
∵CA=CB,CM⊥BA∴BM=AM=$\frac{AB}{2}$=3,
Rt△AMC中,AC=5,AM=3,
∴CF=CM=4,
∴AF=1,
∵CA=CB∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE,
∴$\frac{EA}{BC}=\frac{AF}{BE}$,
设BE长为x,则EA长为6-x
∴$\frac{6-x}{5}=\frac{1}{x}$,
解得:x1=1,x2=5,
答:BE的长为1或5;
(3)可能.如图2,
①当CE=CF时,∠3=∠2=∠A,
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CE=EF时,
又∵△AEF∽△BCE,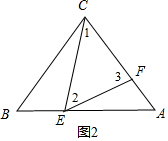
∴△AEF≌△BCE,
∴AE=BC=5,
∴BE=AB-5=1,
③当CF=EF时,∠1=∠2=∠A=∠B,
△FCE∽△CBA,
∴$\frac{EF}{AC}=\frac{CE}{AB}$,
∴$\frac{EF}{CE}$=$\frac{AC}{AB}$=$\frac{5}{6}$,
∵△AEF∽△BCE
∴$\frac{EA}{BC}$=$\frac{EF}{CE}$=$\frac{5}{6}$
∴EA=$\frac{5}{6}$BC=$\frac{5}{6}$×5=$\frac{25}{6}$,
∴EB=AB-$\frac{25}{6}$=$\frac{11}{6}$.
答:当BE的长为1或$\frac{11}{6}$时,△CFE为等腰三角形.
点评 此题考查相似三角形的判定和性质,等腰三角形的判定,直线与圆的位置关系.解答(3)题时,一定要分类讨论,以防漏解.

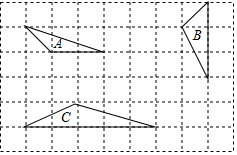 下列三个三角形中相似的是( )
下列三个三角形中相似的是( )| A. | A与B | B. | A与C | C. | B与C | D. | A,B,C都相似 |
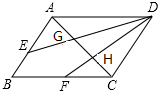 如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.
如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.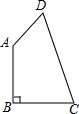 如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.
如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且AB⊥BC于B.