题目内容
9.先化简$\frac{4}{a+3}$-$\frac{6}{{a}^{2}-9}$÷$\frac{2}{a-3}$,再求代数式的值,其中a=$\sqrt{3}$-3.分析 根据分式的除法和减法可以化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:$\frac{4}{a+3}$-$\frac{6}{{a}^{2}-9}$÷$\frac{2}{a-3}$
=$\frac{4}{a+3}-\frac{6}{(a+3)(a-3)}×\frac{a-3}{2}$
=$\frac{4}{a+3}-\frac{3}{a+3}$
=$\frac{1}{a+3}$,
当a=$\sqrt{3}$-3时,原式=$\frac{1}{\sqrt{3}-3+3}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
17.若2(a+3)的值与4互为相反数,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -5 | C. | -$\frac{7}{2}$ | D. | -1 |
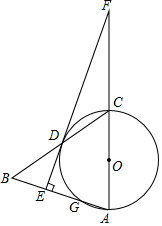 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F. 如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BC=2,连接CD,求BD的长.
如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BC=2,连接CD,求BD的长. 如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形.
如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形. 如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.
如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.