题目内容
12．（1）解方程：x2+6x-7=0（2）解不等式组$\left\{\begin{array}{l}2x+5≤3（x+2）\\ \frac{x-1}{2}＜\frac{x}{3}\end{array}$．
分析 （1）利用因式分解法求解即可；
（2）先解不等式组中的每一个不等式，再求其公共解集即可．
解答 解：（1）原方程变形为（x-1）（x+7）=0，
所以x1=-7，x2=1；
（2）$\left\{\begin{array}{l}{2x+5≤3（x+2）①}\\{\frac{x-1}{2}＜\frac{x}{3}②}\end{array}\right.$，
由①得：x≥-1，
由②得：x＜3，
所以不等式组的解集为：-1≤x＜3．
点评 本题考查了因式分解法解一元二次方程，当把方程通过移项把等式的右边化为0后方程的左边能因式分解时，一般情况下是把左边的式子因式分解，再利用积为0的特点解出方程的根．因式分解法是解一元二次方程的一种简便方法，要会灵活运用．也考查了解一元一次不等式组．
练习册系列答案
名题金卷系列答案
相关题目
2．
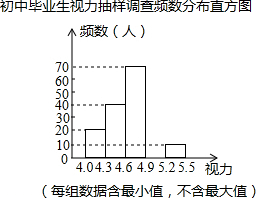某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图，请根据图表信息回答下列问题：
初中毕业生视力抽样调查频数分布表
（1）本次调查的样本容量为200；
（2）在频数分布表中，a=60，b=0.05，并将频数分布直方图补充完整；
（3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图，请根据图表信息回答下列问题：初中毕业生视力抽样调查频数分布表
| 视力 | 频数（人） | 频率 |
| 4.0≤x＜4.3 | 20 | 0.1 |
| 4.3≤x＜4.6 | 40 | 0.2 |
| 4.6≤x＜4.9 | 70 | 0.35 |
| 4.9≤x＜5.2 | a | 0.3 |
| 5.2≤x＜5.5 | 10 | b |
（2）在频数分布表中，a=60，b=0.05，并将频数分布直方图补充完整；
（3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？
17．若2（a+3）的值与4互为相反数，则a的值为（ ）
| A． | $\frac{1}{2}$ | B． | -5 | C． | -$\frac{7}{2}$ | D． | -1 |
如图，⊙O是△ABC的外接圆，∠A=45°，BD是直径，且BC=2，连接CD，求BD的长．
如图，在△ABC中，已知CA=CB=5，BA=6，点E是线段AB上的动点（不与端点重合），点F是线段AC上的动点，连接CE、EF，若在点E、点F的运动过程中，始终保证∠CEF=∠B．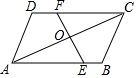
如图，在平行四边形ABCD中，AC的垂直平分线分别交CD，AB于点F和E，AB=4，BC=$\sqrt{3}$，AC=3$\sqrt{3}$，求EF的长．