题目内容
15.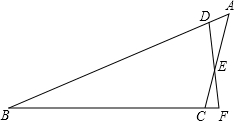 已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.
已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.
分析 作DH∥BC交AC于H,如图,由于$\frac{AD}{AC}$=$\frac{AE}{AB}$=$\frac{1}{4}$,∠DAE=∠CAB,则根据相似三角形的判定可得△ADE∽△ACB,利用相似比可计算出DE=4,再根据平行线分线段成比例定理,由DH∥BC得$\frac{AH}{AC}$=$\frac{DH}{BC}$=$\frac{AD}{AB}$,则可计算出AH=$\frac{4}{5}$,DH=$\frac{8}{5}$,则HE=AE-AH=$\frac{21}{5}$,CE=AC-AE=3,然后由DH∥CF得到$\frac{DE}{EF}$=$\frac{DH}{CF}$=$\frac{EH}{EC}$,则可计算出EF=$\frac{20}{7}$,CF=$\frac{8}{7}$.
解答 解:作DH∥BC交AC于H,如图,
∵AD=2,AE=5,AB=20,AC=8,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$=$\frac{1}{4}$,
而∠DAE=∠CAB,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AD}{AC}$,即$\frac{DE}{16}$=$\frac{2}{8}$,
∴DE=4,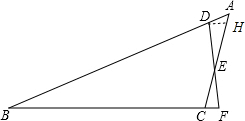
∵DH∥BC,
∴$\frac{AH}{AC}$=$\frac{DH}{BC}$=$\frac{AD}{AB}$,即$\frac{AH}{8}$=$\frac{DH}{16}$=$\frac{2}{20}$,解得AH=$\frac{4}{5}$,DH=$\frac{8}{5}$,
∴HE=AE-AH=5-$\frac{4}{5}$=$\frac{21}{5}$,
而CE=AC-AE=8-5=3,
∵DH∥CF,
∴$\frac{DE}{EF}$=$\frac{DH}{CF}$=$\frac{EH}{EC}$,即$\frac{4}{EF}$=$\frac{\frac{8}{5}}{CF}$=$\frac{\frac{21}{5}}{3}$,
∴EF=$\frac{20}{7}$,CF=$\frac{8}{7}$.
答:△CEF中EC=3,EF=$\frac{20}{7}$,CF=$\frac{8}{7}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了相似三角形的判定与性质.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 以上都不对 |
| A. | 2,3,4 | B. | 3,4,5 | C. | 4,5,5 | D. | 5,5、5 |
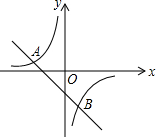 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.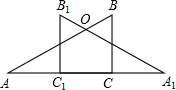 两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.
两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.