题目内容
8.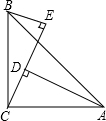 已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
分析 根据∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,求得∠ACD=∠BCE,利用角角边定理可证得△ACD≌△CBE,得出CE=AD,BE=CD=CE-DE,将已知数值代入即可求得答案.
解答 解:∵∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
∴∠ACD=∠ACB-∠BCE=90°-∠BCE,∠CBE=90°-∠BCE(三角形内角和定理),
∴∠ACD=∠CBE,
在△ACD与△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS).
∴CE=AD=2.5cm,BE=DC
∴DC=CE-DE=2.5-1.7=0.8cm
∴BE=0.8cm.
点评 此题考查学生对等腰直角三角形和全等三角形的判定与性质的理解和掌握,关键是利用角角边定理可证得△ACD≌△CBE.

练习册系列答案
相关题目
16.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值是( )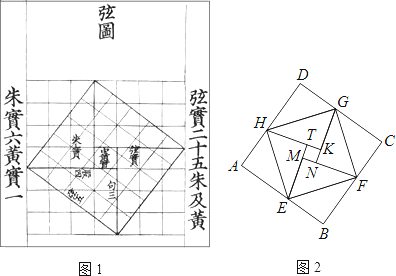

| A. | $\frac{11}{3}$ | B. | $\frac{10}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
17.下列关于正六边形的说法错误的是( )
| A. | 边都相等 | B. | 对角线都相等 | C. | 内角都相等 | D. | 外角都相等 |
 如图,在等边△ABC中,D是边AC上一个动点,连接BD.将线段BD绕点B逆时针旋转60°得到BE,连接ED.若BC=2,则△AED的周长最小值是2+$\sqrt{3}$.
如图,在等边△ABC中,D是边AC上一个动点,连接BD.将线段BD绕点B逆时针旋转60°得到BE,连接ED.若BC=2,则△AED的周长最小值是2+$\sqrt{3}$.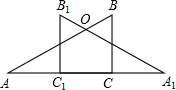 两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.
两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.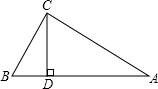 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.
如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.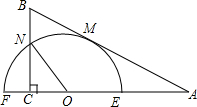 如图,将一块直角三角形纸片和半圆形纸片按图中方式叠放.直角三角形一直角边AC所在直线与半圆O的直径EF所在直线重合,使半圆O与斜边AB切于点M,与BC边交于点N.若重叠部分的弧所对应的圆心角(∠EON)为120°,OC的长为2cm,AE的长为3cm.
如图,将一块直角三角形纸片和半圆形纸片按图中方式叠放.直角三角形一直角边AC所在直线与半圆O的直径EF所在直线重合,使半圆O与斜边AB切于点M,与BC边交于点N.若重叠部分的弧所对应的圆心角(∠EON)为120°,OC的长为2cm,AE的长为3cm.